|
Many physical systems are governed by nonlinear equations whose exact solutions are unavailable. Nevertheless, when the system operates near a point of equilibrium or symmetry, its behavior may be approximated using a power series expansion. The Maclaurin series, a Taylor series expanded about the origin, is
especially useful when the relevant physical variable is naturally small.
Such expansions underpin approximations ranging from the small angle pendulum to harmonic oscillator limits in quantum mechanics and field theory. The power of the Maclaurin series lies not merely in computational convenience, but in its ability to expose the hierarchical structure of physical effects.
Let 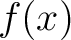 be infinitely differentiable at be infinitely differentiable at 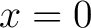 . The Maclaurin series of . The Maclaurin series of 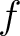 is given by is given by
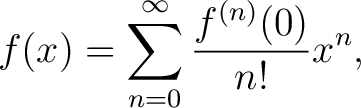 |
(1) |
provided the series converges to 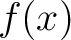 within some radius of convergence. within some radius of convergence.
Truncating the series at finite order 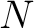 yields an approximation yields an approximation
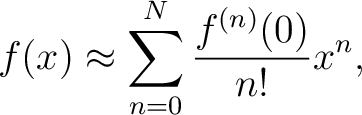 |
(2) |
whose accuracy depends both on 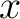 and on the neglected higher order terms. and on the neglected higher order terms.
Consider a simple pendulum of length 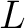 under gravity under gravity 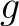 . The exact equation of motion is . The exact equation of motion is
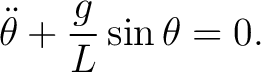 |
(3) |
The nonlinearity arises from the sine term. Expanding
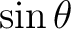 about about
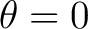 using its Maclaurin series, using its Maclaurin series,
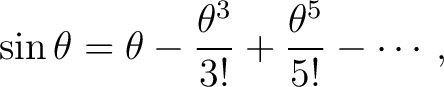 |
(4) |
we obtain, to lowest order,
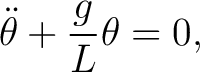 |
(5) |
which describes a simple harmonic oscillator with angular frequency
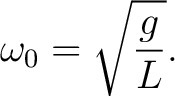 |
(6) |
This approximation is valid when
 (in radians). Retaining the cubic term introduces an anharmonic correction, leading to amplitude dependent oscillation periods. (in radians). Retaining the cubic term introduces an anharmonic correction, leading to amplitude dependent oscillation periods.
More generally, consider a particle of mass 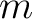 moving in a one dimensional potential moving in a one dimensional potential 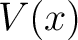 with a stable equilibrium at with a stable equilibrium at 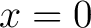 . The potential may be expanded as . The potential may be expanded as
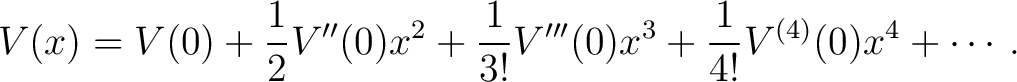 |
(7) |
The absence of a linear term reflects equilibrium. The quadratic term defines an effective harmonic oscillator with angular frequency
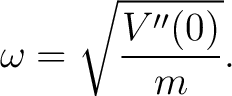 |
(8) |
Higher order terms introduce anharmonic effects, modifying both classical trajectories and quantum energy levels. The Maclaurin expansion thus provides a systematic route from exact dynamics to effective models.
In quantum mechanics, the Hamiltonian
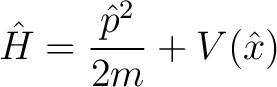 |
(9) |
may be approximated near equilibrium by truncating the Maclaurin expansion of 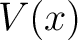 . Retaining only the quadratic term yields the harmonic oscillator, whose eigenstates and spectrum are exactly solvable. . Retaining only the quadratic term yields the harmonic oscillator, whose eigenstates and spectrum are exactly solvable.
Including quartic corrections,
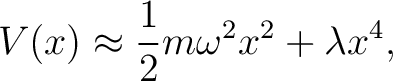 |
(10) |
leads to perturbative shifts in the energy levels. These corrections can be computed using standard perturbation theory, illustrating how Maclaurin expansions connect directly to observable physical effects.
The Maclaurin series is local by construction. Its validity is constrained by both convergence and physical relevance. Even when the series converges mathematically, truncation may fail to capture qualitative behavior such as bifurcations or chaotic dynamics.
Thus, Maclaurin expansions should be interpreted as controlled approximations, whose domain of applicability must be justified physically, not merely algebraically.
The Maclaurin series is far more than a mathematical curiosity; it is a foundational tool in physical modeling. By expanding physical laws about equilibrium points, one obtains effective theories that isolate dominant behavior while systematically accounting for corrections. From classical mechanics to quantum theory, the Maclaurin series provides a bridge between exact laws and practical predictions.
- 1
- G. B. Arfken, H. J. Weber, and F. E. Harris, Mathematical Methods for Physicists, 7th ed., Academic Press, 2013.
- 2
- H. Goldstein, C. Poole, and J. Safko, Classical Mechanics, 3rd ed., Addison-Wesley, 2002.
- 3
- L. D. Landau and E. M. Lifshitz, Mechanics, 3rd ed., Butterworth-Heinemann, 1976.
- 4
- D. J. Griffiths, Introduction to Quantum Mechanics, 2nd ed., Pearson Prentice Hall, 2005.
- 5
- J. J. Sakurai and J. Napolitano, Modern Quantum Mechanics, 2nd ed., Pearson, 2011.
- 6
- M. L. Boas, Mathematical Methods in the Physical Sciences, 3rd ed., Wiley, 2006.
|

