|
A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered. It is named after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.
The Taylor series of a real or complex-valued function
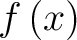 , that is infinitely differentiable at a real or complex number , that is infinitely differentiable at a real or complex number 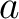 , is the power series , is the power series
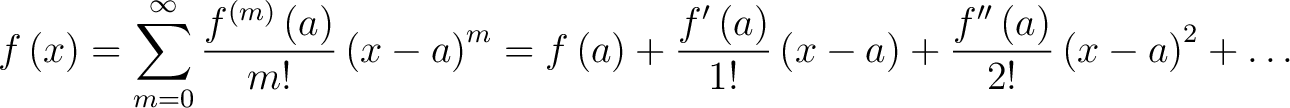 |
(1) |
Here,  denotes the factorial of denotes the factorial of 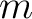 . The function . The function
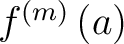 denotes the denotes the  th derivative of th derivative of 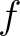 evaluated at the point evaluated at the point 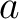 . The derivative of order zero of . The derivative of order zero of 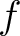 is defined to be is defined to be 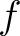 itself and itself and
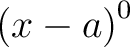 and and 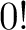 are both defined to be are both defined to be 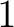 . With . With 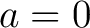 , the Maclaurin series takes the form: , the Maclaurin series takes the form:
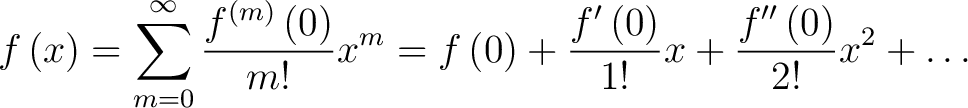 |
(2) |
This article is a derivative work of the creative commons share alike with attribution in [1].
- [1] Wikipedia contributors, “Taylor series,” Wikipedia, The Free Encyclopedia. Accessed July 13, 2025.
[2] Kreyszig, E., “Advanced Engineering Mathematics.” Fifth Edition. John Wiley and Sons, Inc. 1983.
|

