|
In mathematics, a power series (in one variable) is an infinite series of the form
 |
(1) |
where 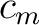 represents the coefficient of the represents the coefficient of the 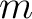 th term and th term and  is a constant called the center of the series. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function. is a constant called the center of the series. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function.
In many situations, the center 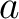 is equal to zero, for instance for Maclaurin series. In such cases, the power series takes the simpler form is equal to zero, for instance for Maclaurin series. In such cases, the power series takes the simpler form
 |
(2) |
The partial sums of a power series are polynomials, the partial sums of the Taylor series of an analytic function are a sequence of converging polynomial approximations to the function at the center, and a converging power series can be seen as a kind of generalized polynomial with infinitely many terms. Conversely, every polynomial is a power series with only finitely many non-zero terms.
Power series are powerful for solving differential equations and can be useful when considering variable coefficients over other methods. Beyond their role in mathematical analysis, power series also occur in combinatorics as generating functions (a kind of formal power series) and in electronic engineering (under the name of the 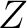 -transform). The familiar decimal notation for real numbers can also be viewed as an example of a power series, with integer coefficients, but with the argument -transform). The familiar decimal notation for real numbers can also be viewed as an example of a power series, with integer coefficients, but with the argument 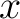 fixed at fixed at
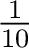 . In number theory, the concept of . In number theory, the concept of  -adic numbers is also closely related to that of a power series. -adic numbers is also closely related to that of a power series.
This article is a derivative work of the creative commons share alike with attribution in [1].
- [1] Wikipedia contributors, “Power series,” Wikipedia, The Free Encyclopedia. Accessed July 13, 2025.
[2] Kreyszig, E., “Advanced Engineering Mathematics.” Fifth Edition. John Wiley and Sons, Inc. 1983.
|

