|
In physics, the resultant force is the single force that represents the combined effect of multiple forces acting on an object. Forces are vector quantities, characterized by both magnitude and direction. To find the resultant force, we add the individual force vectors using vector addition.
Consider an object subjected to two forces:
-
 N at N at  (along the positive (along the positive 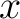 -axis). -axis).
-
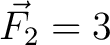 N at N at 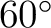 from the positive from the positive 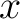 -axis. -axis.
We aim to find the resultant force
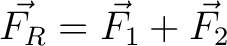 . .
Express each force in terms of its 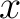 - and - and 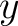 -components: -components:
The components of the resultant force
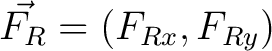 are: are:
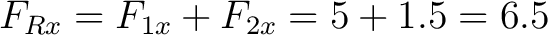 N  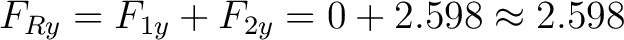 N  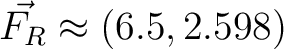 N. N.
The magnitude of 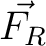 is: is:
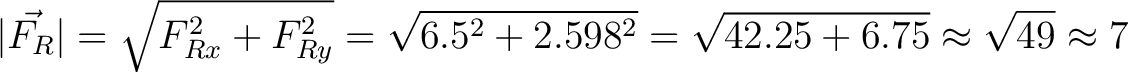 N  The direction (angle 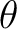 relative to the positive relative to the positive 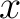 -axis) is: -axis) is:
Thus, the resultant force is approximately
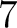 N at N at
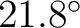 from the positive from the positive  -axis. -axis.
The following diagram illustrates the two forces and their resultant:
This example was generated by Grok, an AI developed by xAI, on June 6, 2025.
| 
