|
Electrical power is the rate at which electrical energy is delivered or consumed in a circuit. If a device has an electrical potential difference denoted by 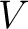 and current denoted by and current denoted by 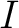 , then the instantaneous electrical power , then the instantaneous electrical power 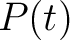 is defined as is defined as
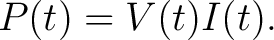 |
(1) |
The SI unit of 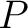 is the watt, denoted is the watt, denoted
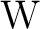 , where one watt equals one joule per second. , where one watt equals one joule per second.
Consider a simple series circuit consisting of a voltage source 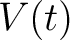 and a resistor and a resistor 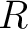 . For a purely resistive load, the current and voltage are in phase and Ohm laws applies at every instant: . For a purely resistive load, the current and voltage are in phase and Ohm laws applies at every instant:
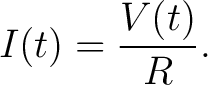 |
(2) |
We will assume that the source voltage is sinusoidal of angular frequency 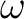 and amplitude and amplitude 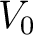 , so that , so that
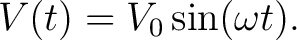 |
(3) |
Substituting into Ohms law gives the instantaneous current:
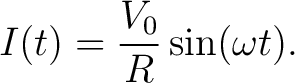 |
(4) |
Using the definitions above, the instantaneous power delivered to the resistor is
This equation shows that the instantaneous power oscillates at twice the fundamental frequency. The power is always nonnegative for a resistive load, consistent with the fact that a resistor only consumes energy, it does not return energy to the source.
The average power
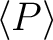 over one full cycle is obtained by integrating over one full cycle is obtained by integrating 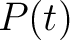 with respect to time over the period with respect to time over the period
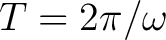 and dividing by the period: and dividing by the period:
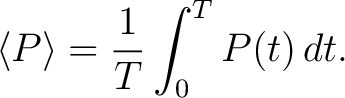 |
(8) |
Substituting 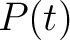 yields yields
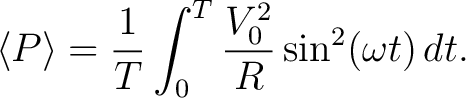 |
(9) |
Using the trigonometric identity
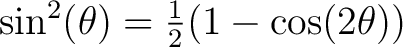 , we find , we find
The cosine term averages to zero over a full cycle, leaving one half of the peak squared divided by the resistance.
It is common to express average power in terms of root mean square (rms) values. Define the rms voltage
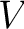 rms and rms current rms and rms current
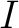 rms as rms as
Using these definitions, the average power becomes
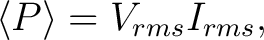 |
(14) |
which is the standard form used in circuit analysis.
In our example, the voltage and current are in phase, so the average power represents real energy delivered to the resistor each second. The average power in watts equals the rate of conversion of electrical energy into heat in the resistor.
We computed the instantaneous and average electrical power delivered to a resistive element in response to a sinusoidal source. The average power is one half the peak voltage squared divided by the resistance and may be expressed as the product of rms voltage and rms current. These results are standard in electrical engineering and physics and provide a basis for more complex analysis of circuits with time varying sources.
- 1
- C. K. Alexander and M. N. O. Sadiku, Fundamentals of Electric Circuits, 6th edition, McGraw Hill, 2016.
- 2
- J. W. Nilsson and S. A. Riedel, Electric Circuits, 10th edition, Pearson, 2019.
- 3
- R. L. Boylestad, Introductory Circuit Analysis, 14th edition, Pearson, 2018.
| 
