|
Geiger's Method
|
(Definition)
|
|
|
Geiger's method [1] is an iterative procedure using Gauss-Newton optimization to determine the location of an earthquake, or seismic event. Originally his method was developed to obtain the origin time and Epicentre but it is easily extended to include the Focal Depth for Hypocentre determination.
Given a set of 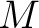 arrival times arrival times 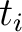 find the origin time find the origin time 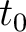 and the hypocentre in cartesian coordinatios and the hypocentre in cartesian coordinatios
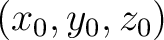 which minimize the objective function which minimize the objective function
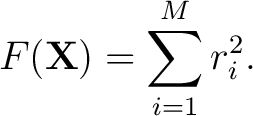 |
(1) |
Here, 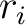 is the difference between observed and calculated arrival times is the difference between observed and calculated arrival times
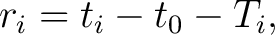 |
(2) |
and the unknown parameter vector is
 |
(3) |
In matrix form (1) becomes
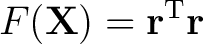 |
(4) |
The Gauss–Newton procedure requires an initial guess of the sought parameters, denoted here as
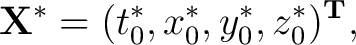 |
(5) |
which are then used to calculate the adjustment vector
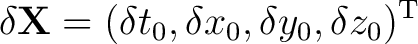 |
(6) |
in
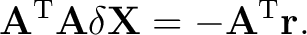 |
(7) |
The Jacobian matrix
 is defined as is defined as
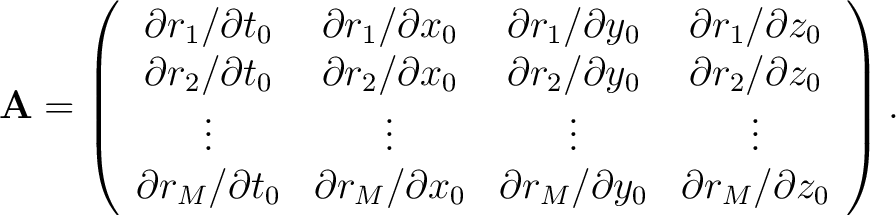 |
(8) |
The partial derivatives are evaluated at the initial guess, or trial vector,
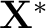 . Equation (7) can be rewritten as . Equation (7) can be rewritten as
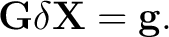 |
(9) |
Using (9) and an initial guess
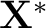 an adjustment vector can be calculated. The initial guess can then be updated an adjustment vector can be calculated. The initial guess can then be updated
 and used as the inital guess in the next run of the algorithm. In this manner the sought parameters and used as the inital guess in the next run of the algorithm. In this manner the sought parameters
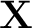 can be determined to some tolerance. can be determined to some tolerance.
- 1
- Geiger, L., “Probability method for the determination of earthquake epicenters from the arrival time only.” Bull. St. Louis Univ. vol. 8, pp. 60-71.
- 2
- Lee, W. H. K. and Stewart, S. W. Principles and Applications of Microearthquake Networks, Academic Press, New York. 1981
- 3
- Gibowicz, S. J. and Kijko, A. An Introduction to Mining Seismology, Academic Press, New York. 1994.
|
"Geiger's Method" is owned by aerringt.
|
|
| Keywords: |
earthquake location, least squares, Gauss-Newton |
Cross-references: algorithm, matrix, vector, parameter, function, Hypocentre, Focal Depth, Epicentre
This is version 2 of Geiger's Method, born on 2006-03-24, modified 2006-03-24.
Object id is 138, canonical name is GeigersMethod.
Accessed 2872 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

