|
We start with the moment of inertia about the origin for the system of particles, which is defined as
 |
(1) |
Differentiate using the chain rule. Note that a vector dotted into itself yields its magnitude square.
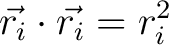 |
(2) |
This lets us make the connection that
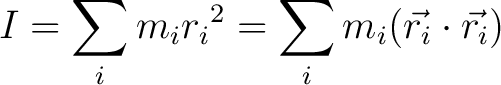 |
(3) |
So after differentiating we get
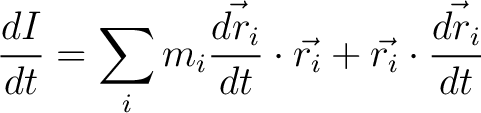 |
(4) |
Differentiating again yields
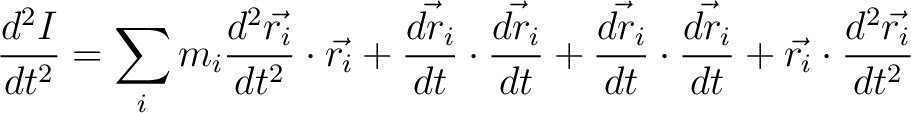 |
(5) |
In short form
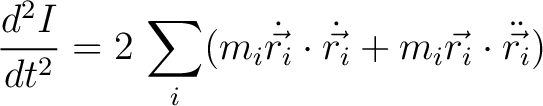 |
(6) |
When dealing with a system of particles we found that the kinetic energy associated with a system of particles was
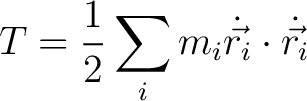 |
(7) |
Plugging in T into (6) gives us
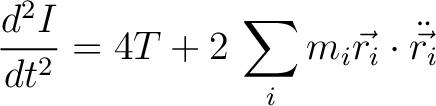 |
(8) |
Next we need to tackle the
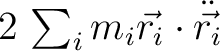 term. We first bring in the potential energy through its connection with force. This part is named the Virial of Claussius. term. We first bring in the potential energy through its connection with force. This part is named the Virial of Claussius.
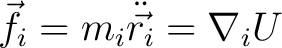 |
(9) |
This gives us the equality
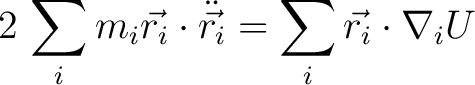 |
(10) |
Now due to Newton's 3rd law that states for every action there is an opposite and equal reaction we have the forces on the ith particle in our system given by
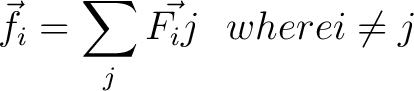 |
(11) |
So when we go to sum up all the forces we notice 'force pairing' such that
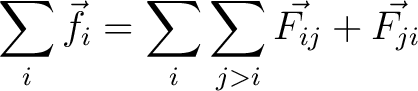 |
(12) |
Plugging this into the virial of Claussius yields
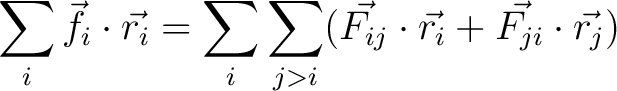 |
(13) |
Now we need to take the gradient of the potential energy to get the force. This is a tedious calculation which can be found here (insert link)
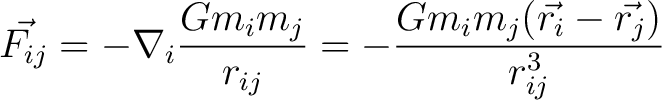 |
(14) |
Inserting this into (13) gives
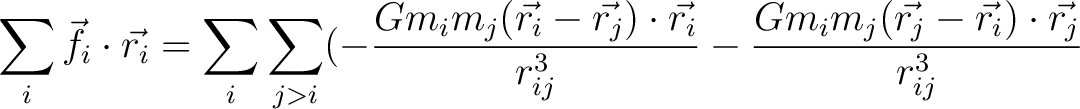 |
(15) |
The two keys in understanding the above equation is to note that
 |
(16) |
and that
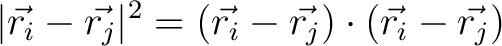 |
(17) |
So now we add the numerators of (15) to get
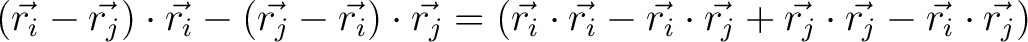 |
(18) |
Next we expand (17) to see that it is equal to (18) and this cancels a power of 2 in the denominator of (15) to finally yeild the expression for potential energy
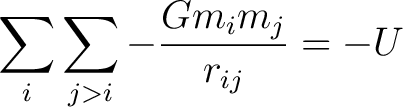 |
(19) |
So going back to (8) we see
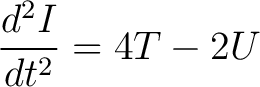 |
(20) |
From the energy equation of the system, E = T - U and the key to finish up the virial theorem is to note that the momemt of inertia does not change on average with time ("After one dynamical timescale, the time derivative of I is constant so the second derivative is zero
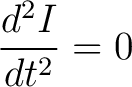 |
(21) |
This leads to
 |
(22) |
plugging this into the energy equation gives us the result of the virial theorem which states that the total energy of a stationary system (no significant dynamical evolution) is one-half the potential energy of the system.
 |
(23) |
| 
