|
From the definition of a contravariant vector (contravariant tensor of rank 1)
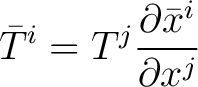 |
(1) |
we get the transformation matrix from the partial derivatives
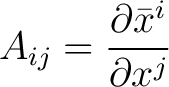 |
(2) |
In order to calculate the transformation matrix, we need the equations relating the two coordinates systems. For cartesian to polar, we have
and for polar to cartesian
So if we designate 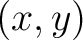 as the bar coordinates, then the transformation components from polar coordinates as the bar coordinates, then the transformation components from polar coordinates
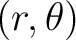 to cartesian coordinates to cartesian coordinates 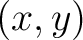 is calculted as is calculted as
The components from cartesian coordinates to polar coordinates transform the same way, but now the polar coordinates have the bar
In summary, the components of contravariant vectors in cartesian coordinates and polar coordinates transform between each other according to
| 
