|
In mathematics, a set is a collection of different things; the things are elements or members of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets themselves are purely conceptual. This is an important point to note: the set of all cows (for example) does not physically exist, even though the cows do. The set is a "gathering" of the cows into one conceptual unit that is not part of physical reality. This makes it easy to see why we can have sets with an infinite number of elements; even though we may not be able to point out infinitely many objects in the real world, we can construct conceptual sets which an infinite number of elements.
Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo-Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century.
If 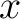 is an element of a set is an element of a set 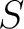 , one says that , one says that 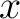 belongs to belongs to  or is in or is in  , and this is written as , and this is written as
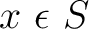 [11]. The statement " [11]. The statement "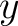 is not in is not in 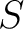 " is written as " is written as
 , which can also be read as " , which can also be read as "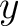 is not in S"[12][13]. For example, if is not in S"[12][13]. For example, if
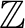 is the set of the integers, one has is the set of the integers, one has
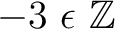 and and
 . Each set is uniquely characterized by its elements. . Each set is uniquely characterized by its elements.
This implies that there is only one set with no element, the empty set (or null set) that is denoted
 , , 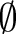 or or 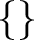 [17][18]. A singleton is a set with exactly one element. If [17][18]. A singleton is a set with exactly one element. If 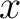 is this element, the singleton is denoted is this element, the singleton is denoted 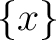 . An element of a set can be itself a set. For example, the singleton . An element of a set can be itself a set. For example, the singleton
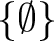 is a set that has the empty set is a set that has the empty set 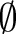 as its unique element. Since these two sets do not have the same elements, as its unique element. Since these two sets do not have the same elements,
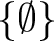 and and 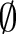 are different sets. are different sets.
A set is finite if there exists a natural number 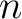 such that the such that the 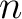 first natural numbers can be put in one to one correspondence with the elements of the set. In this case, one says the first natural numbers can be put in one to one correspondence with the elements of the set. In this case, one says the  is the number of elements of the set. A set is infinite if such an is the number of elements of the set. A set is infinite if such an 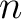 does not exist. The empty set is a finite set with 0 elements. does not exist. The empty set is a finite set with 0 elements.
The natural numbers form an infinite set, commonly denoted
 . Other examples of infinite sets include integer numbers . Other examples of infinite sets include integer numbers
 , rational numbers , rational numbers
 , real numbers , real numbers
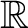 , real vector spaces, curves and most sorts of mathematical spaces. , real vector spaces, curves and most sorts of mathematical spaces.
Extensionality implies that for specifying a set, one has either to list its elements or to provide a property that uniquely characterizes the set elements.
Roster or enumeration notation is a notation introduced by Ernst Zermelo in 1908 that specifies a set by listing its elements between braces, separated by commas [19][20][21][22][23]. For example, one knows that
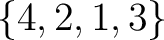 and and
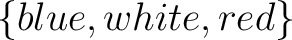 denote sets and not tuples because of the enclosing braces. denote sets and not tuples because of the enclosing braces.
Above notations 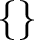 and and 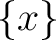 for they empty set and for a singleton are examples of roster notation. for they empty set and for a singleton are examples of roster notation.
When specifying sets, it only matters whether each distinct element is in the set or not; this means a set does not change if elements are repeated for arranged in a different order. For example, [24][25][26]
When there is a clear pattern for generating all set elements, one can use ellipses for abbreviating the notation, [27][28] such as in
for the positive integers not greater than 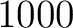 . .
Ellipses allow also expanding roster notation to some infinite sets. For example, the set of all integers can be denoted as
or
Set-builder notation specifies a set as being the set of all elements that satisfy some logical formula [29][30][31]. More precisely if 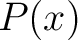 is a logical formula depending on a variable is a logical formula depending on a variable  , which evaluates to true or false depending on the value of , which evaluates to true or false depending on the value of 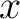 , then , then
This article is a derivative work of the creative commons share alike with attribution in [1].
- [1] Wikipedia contributors. Set (mathematics). Wikipedia, The Free Encyclopedia; [cited 2025 Nov 22].
| 
