|
Here we look at two cases for the moment of inertia of a homogeneous circular disk
(a) about its geometrical axis,
(b) about one of the elements of its lateral surface.
Let m be the mass, a the radius, l the thickness, and 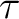 the density of the disk. Then choosing a circular ring for the element of mass we have the density of the disk. Then choosing a circular ring for the element of mass we have
where 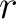 is the radius of the ring and is the radius of the ring and 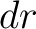 its thickness. its thickness.
Therfore the moment of inertia about the axis of the disk is
The moment of inertia about the element is obtained easily by the help of theorem II. Thus
It will be noticed that the thickness of the disk does not enter into the expressions for 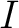 and and 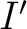 except through the mass of the disk. Therefore these expressions hold good whether the disk is thick enough to be called a cylinder or thin enough to be called a circular lamina. except through the mass of the disk. Therefore these expressions hold good whether the disk is thick enough to be called a cylinder or thin enough to be called a circular lamina.
This article is a derivative of the public domain book, "Analytical mechanics" by Haroutune M. Dadourian, 1913. Made available by the internet archive
| 
