|
One of the simplest Machlaurin series examples is the function
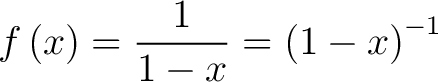 |
(1) |
Apply the chain rule to get the derivatives
Evaluating the function and its derivatives at zero yields
Using the formula for the Machlaurin series
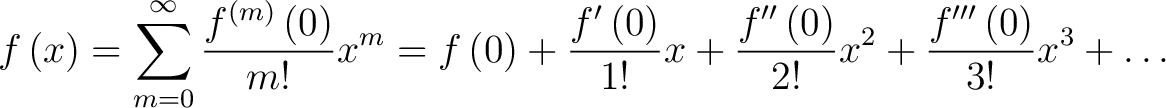 |
(2) |
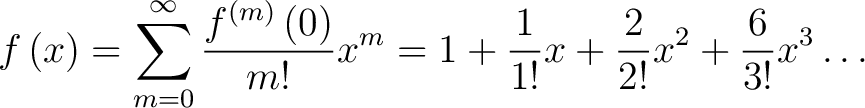 |
(3) |
Finally, evaluating the factorials and seeing they divide out the numerator we get the series
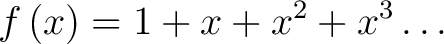 |
(4) |
Let's evaluate example 1 function at 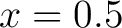 and see how the order of the series (powers of x, so order 3 would go through and see how the order of the series (powers of x, so order 3 would go through 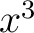
Figure: Example 1 at 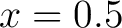
|
|
Another popular example for the Machlaurin series is the function
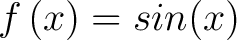 |
(5) |
Get the derivatives, do you see a pattern?
Evaluating the function and its derivatives at zero yields
Using the formula for the Machlaurin series
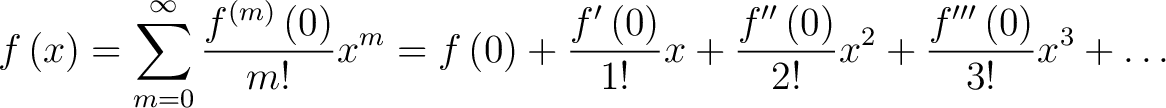 |
(6) |
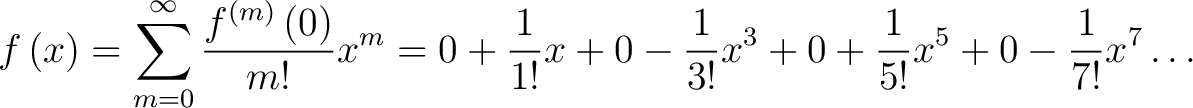 |
(7) |
Finally, evaluating the factorials we get the series
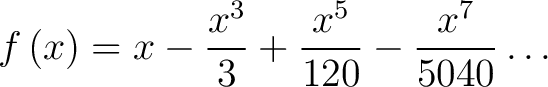 |
(8) |
- [1] Kreyszig, E., “Advanced Engineering Mathematics.” Fifth Edition. John Wiley and Sons, Inc. 1983.
| 
