|
Van Kampen Theorem for groups and groupoids
|
(Theorem)
|
|
|
Van Kampen's theorem for fundamental groups is stated as follows:
Usually the morphisms induced by inclusion in this theorem are not themselves injective, and the more precise version of the statement is in terms of pushouts of groups.
The notion of pushout in the category of groupoids allows for a version of the theorem for the non path connected case, using the fundamental groupoid
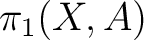 on a set on a set 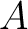 of base points, [1]. This groupoid consists of homotopy classes rel end points of paths in of base points, [1]. This groupoid consists of homotopy classes rel end points of paths in 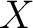 joining points of joining points of 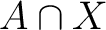 . In particular, if . In particular, if  is a contractible space, and is a contractible space, and 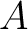 consists of two distinct points of consists of two distinct points of 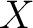 , then , then
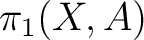 is easily seen to be isomorphic to the groupoid often written is easily seen to be isomorphic to the groupoid often written
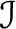 with two vertices and exactly one morphism between any two vertices. This groupoid plays a role in the theory of groupoids analogous to that of the group of integers in the theory of groups. with two vertices and exactly one morphism between any two vertices. This groupoid plays a role in the theory of groupoids analogous to that of the group of integers in the theory of groups.
The interpretation of this theorem as a calculational tool for fundamental groups needs some development of `combinatorial groupoid theory', [2,4]. This theorem implies the calculation of the fundamental group of the circle as the group of integers, since the group of integers is obtained from the groupoid
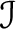 by identifying, in the category of groupoids, its two vertices. by identifying, in the category of groupoids, its two vertices.
There is a version of the last theorem when 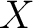 is covered by the union of the interiors of a family is covered by the union of the interiors of a family
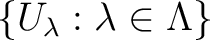 of subsets, [3]. The conclusion is that if of subsets, [3]. The conclusion is that if 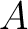 meets each path component of all 1,2,3-fold intersections of the sets meets each path component of all 1,2,3-fold intersections of the sets 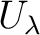 , then A meets all path components of , then A meets all path components of 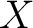 and the diagram and the diagram
of morphisms induced by inclusions is a coequaliser in the category of groupoids.
- 1
- R. Brown, “Groupoids and Van Kampen's theorem”, Proc. London Math. Soc. (3) 17 (1967) 385-401.
- 2
- R. Brown, Topology and Groupoids, Booksurge PLC (2006).
- 3
- R. Brown and A. Razak, “A van Kampen theorem for unions of non-connected spaces”, Archiv. Math. 42 (1984) 85-88.
- 4
- P.J. Higgins, Categories and Groupoids, van Nostrand, 1971, Reprints of Theory and Applications of Categories, No. 7 (2005) pp 1-195.
|
"Van Kampen Theorem for groups and groupoids" is owned by bci1.
|
|
See Also: generalized Van Kampen theorems (HD-GVKT) -- higher dimensional
| Also defines: |
fundamental groups, pushout |
| Keywords: |
frundamental groups, pushouts, Van Kampen's theorem for groups, topological spaces, algebraic topology |
Cross-references: homotopy, groupoid, fundamental groupoid, category of groupoids, groups, injective, isomorphism, diagram, morphisms, union, topological, theorem
There are 9 references to this object.
This is version 18 of Van Kampen Theorem for groups and groupoids, born on 2010-12-13, modified 2010-12-13.
Object id is 899, canonical name is VanKampenTheoremForGroupsAndGroupoids.
Accessed 2405 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

