|
A compact quantum group, 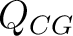 is defined as a particular case of a locally compact quantum group is defined as a particular case of a locally compact quantum group 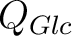 when the object space of the latter when the object space of the latter 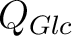 is a compact topological space (instead of being a locally compact one). is a compact topological space (instead of being a locally compact one).
Bibliography
![$[1]$ $[1]$](http://images.physicslibrary.org/cache/objects/311/l2h/img4.png) ABE, E., Hopf Algebras, Cambridge University Press, 1977. ABE, E., Hopf Algebras, Cambridge University Press, 1977.
![$[2]$ $[2]$](http://images.physicslibrary.org/cache/objects/311/l2h/img5.png) BAAJ, S., SKANDALIS, G., Unitaires multiplicatifs et dualité pour les produits croisés de C*-algébres, Ann. scient. Ec. Norm. Sup., 4e série, t. 26 (1993), 425-488. BAAJ, S., SKANDALIS, G., Unitaires multiplicatifs et dualité pour les produits croisés de C*-algébres, Ann. scient. Ec. Norm. Sup., 4e série, t. 26 (1993), 425-488.
![$[3]$ $[3]$](http://images.physicslibrary.org/cache/objects/311/l2h/img6.png) CONWAY, J. B., A Course in Functional Analysis, Springer-Verlag, New York, 1985. CONWAY, J. B., A Course in Functional Analysis, Springer-Verlag, New York, 1985.
![$[4]$ $[4]$](http://images.physicslibrary.org/cache/objects/311/l2h/img7.png) DIJKHUIZEN, M.S., KOORNWINDER, T.H., CQG algebras : a direct algebraic approach to quantum groups, Lett. Math. Phys. 32 (1994), 315-330. DIJKHUIZEN, M.S., KOORNWINDER, T.H., CQG algebras : a direct algebraic approach to quantum groups, Lett. Math. Phys. 32 (1994), 315-330.
![$[5]$ $[5]$](http://images.physicslibrary.org/cache/objects/311/l2h/img8.png) DIXMIER, J., C*-algebras, North-Holland Publishing Company, Amsterdam, 1982. DIXMIER, J., C*-algebras, North-Holland Publishing Company, Amsterdam, 1982.
![$[6]$ $[6]$](http://images.physicslibrary.org/cache/objects/311/l2h/img9.png) ENOCK, M., SCHWARTZ, J.-M., Kac Algebras and duality of Locally Compact groups, Springer-Verlag, Berlin (1992). ENOCK, M., SCHWARTZ, J.-M., Kac Algebras and duality of Locally Compact groups, Springer-Verlag, Berlin (1992).
![$[7]$ $[7]$](http://images.physicslibrary.org/cache/objects/311/l2h/img10.png) EFFROS, E.G., RUAN, Z.-J., Discrete Quantum Groups I. The Haar measure, Int. J. of Math. (1994), 681-723. EFFROS, E.G., RUAN, Z.-J., Discrete Quantum Groups I. The Haar measure, Int. J. of Math. (1994), 681-723.
![$[8]$ $[8]$](http://images.physicslibrary.org/cache/objects/311/l2h/img11.png) HOFMANN, K.H., Elements of compact semi-groups, Charles E. Merill Books Inc. Columbus, Ohio (1996). HOFMANN, K.H., Elements of compact semi-groups, Charles E. Merill Books Inc. Columbus, Ohio (1996).
![$[9]$ $[9]$](http://images.physicslibrary.org/cache/objects/311/l2h/img12.png) HOLLEVOET, J., Lokaal compacte quantum-semigroepen : Representaties en Pontryagin-dualiteit, Ph.D. Thesis, K.U.Leuven, 1994. HOLLEVOET, J., Lokaal compacte quantum-semigroepen : Representaties en Pontryagin-dualiteit, Ph.D. Thesis, K.U.Leuven, 1994.
![$[10]$ $[10]$](http://images.physicslibrary.org/cache/objects/311/l2h/img13.png) HOLLEVOET, J., Pontryagin Duality for a Class of Locally Compact Quantum Groups, Math. Nachrichten 176 (1995), 93-110. HOLLEVOET, J., Pontryagin Duality for a Class of Locally Compact Quantum Groups, Math. Nachrichten 176 (1995), 93-110.
![$[11]$ $[11]$](http://images.physicslibrary.org/cache/objects/311/l2h/img14.png) KIRCHBERG, E., Discrete Quantum Groups, talk at Oberwolfach, 1994. KIRCHBERG, E., Discrete Quantum Groups, talk at Oberwolfach, 1994.
![$[12]$ $[12]$](http://images.physicslibrary.org/cache/objects/311/l2h/img15.png) KUSTERMANS, J., C*-algebraic Quantum Groups arising from Algebraic Quantum Groups, Ph.D. Thesis, K.U.Leuven, 1997. KUSTERMANS, J., C*-algebraic Quantum Groups arising from Algebraic Quantum Groups, Ph.D. Thesis, K.U.Leuven, 1997.
![$[13]$ $[13]$](http://images.physicslibrary.org/cache/objects/311/l2h/img16.png) KUSTERMANS, J., VAN DAELE, A., C*-algebraic Quantum Groups arising from Algebraic Quantum Groups, Int. J. of Math. 8 (1997), 1067-1139. KUSTERMANS, J., VAN DAELE, A., C*-algebraic Quantum Groups arising from Algebraic Quantum Groups, Int. J. of Math. 8 (1997), 1067-1139.
![$[14]$ $[14]$](http://images.physicslibrary.org/cache/objects/311/l2h/img17.png) LANCE, E.C., An explicit description of the fundamental unitary for SU(2)q, Commun. Math. Phys. 164 (1994), 1-15. LANCE, E.C., An explicit description of the fundamental unitary for SU(2)q, Commun. Math. Phys. 164 (1994), 1-15.
![$[15]$ $[15]$](http://images.physicslibrary.org/cache/objects/311/l2h/img18.png) DE MAGELHAES, I.V., Hopf-C*-algebras and locally compact groups, Pacific J. Math (2) 36 (1935), 448-463. DE MAGELHAES, I.V., Hopf-C*-algebras and locally compact groups, Pacific J. Math (2) 36 (1935), 448-463.
![$[16]$ $[16]$](http://images.physicslibrary.org/cache/objects/311/l2h/img19.png) MASUDA, M., NAKAGAMI, Y., A von Neumann algebra Framework for the Duality of Quantum Groups. Publications of the RIMS Kyoto University 30 (1994), 799-850. MASUDA, M., NAKAGAMI, Y., A von Neumann algebra Framework for the Duality of Quantum Groups. Publications of the RIMS Kyoto University 30 (1994), 799-850.
![$[17]$ $[17]$](http://images.physicslibrary.org/cache/objects/311/l2h/img20.png) MASUDA, M., A C*-algebraic framework for the quantum groups, talk at Warsaw workshop on Quantum Groups and Quantum Spaces, 1995. MASUDA, M., A C*-algebraic framework for the quantum groups, talk at Warsaw workshop on Quantum Groups and Quantum Spaces, 1995.
![$[18]$ $[18]$](http://images.physicslibrary.org/cache/objects/311/l2h/img21.png) MASUDA, M., NAKAGAMI, Y., WORONOWICZ, , S.L. (in preparation). MASUDA, M., NAKAGAMI, Y., WORONOWICZ, , S.L. (in preparation).
![$[19]$ $[19]$](http://images.physicslibrary.org/cache/objects/311/l2h/img22.png) SHEU, A.J.L., Compact Quantum Groups and groupoid C*-Algebras, J. Funct. Analysis 144 (1997), 371-393. SHEU, A.J.L., Compact Quantum Groups and groupoid C*-Algebras, J. Funct. Analysis 144 (1997), 371-393.
![$[20]$ $[20]$](http://images.physicslibrary.org/cache/objects/311/l2h/img23.png) SWEEDLER, M.E., Hopf Algebras, W.A. Benjamin, inc., New York, 1969. SWEEDLER, M.E., Hopf Algebras, W.A. Benjamin, inc., New York, 1969.
![$[21]$ $[21]$](http://images.physicslibrary.org/cache/objects/311/l2h/img24.png) TOMIYAMA, J., Applications of Fubini type theorems to the tensor product of C*-algebras, Tokohu Math. J. 19 (1967), 213-226. TOMIYAMA, J., Applications of Fubini type theorems to the tensor product of C*-algebras, Tokohu Math. J. 19 (1967), 213-226.
![$[22]$ $[22]$](http://images.physicslibrary.org/cache/objects/311/l2h/img25.png) VAN DAELE, A., Dual Pairs of Hopf *-algebras, Bull. London Math. Soc. 25 (1993), 209-230. VAN DAELE, A., Dual Pairs of Hopf *-algebras, Bull. London Math. Soc. 25 (1993), 209-230.
![$[23]$ $[23]$](http://images.physicslibrary.org/cache/objects/311/l2h/img26.png) VAN DAELE, A., Multiplier Hopf Algebras, Trans. Am. Math. Soc. 342 (1994), 917-932. VAN DAELE, A., Multiplier Hopf Algebras, Trans. Am. Math. Soc. 342 (1994), 917-932. ![$[24]$ $[24]$](http://images.physicslibrary.org/cache/objects/311/l2h/img27.png) VAN DAELE, A., The Haar Measure on a Compact Quantum Group, Proc. Amer. Math. Soc. 123 (1995), 3125-3128. VAN DAELE, A., The Haar Measure on a Compact Quantum Group, Proc. Amer. Math. Soc. 123 (1995), 3125-3128. ![$[25]$ $[25]$](http://images.physicslibrary.org/cache/objects/311/l2h/img28.png) VAN DAELE, A., Discrete Quantum Groups, Journal of Algebra 180 (1996), 431-444. VAN DAELE, A., Discrete Quantum Groups, Journal of Algebra 180 (1996), 431-444. ![$[26]$ $[26]$](http://images.physicslibrary.org/cache/objects/311/l2h/img29.png) VAN DAELE, A., An Algebraic Framework for Group Duality, preprint K.U.Leuven (1996), to appear in Advances of Mathematics. VAN DAELE, A., An Algebraic Framework for Group Duality, preprint K.U.Leuven (1996), to appear in Advances of Mathematics.
![$[27]$ $[27]$](http://images.physicslibrary.org/cache/objects/311/l2h/img30.png) VAN DAELE, A., Multiplier Hopf Algebras and Duality, Proceedings of the workshop on Quantum Groups and Quantum Spaces in Warsaw (1995), Polish Academy of sciences Warszawa 40 (1997), 51-58. VAN DAELE, A., Multiplier Hopf Algebras and Duality, Proceedings of the workshop on Quantum Groups and Quantum Spaces in Warsaw (1995), Polish Academy of sciences Warszawa 40 (1997), 51-58.
![$[28]$ $[28]$](http://images.physicslibrary.org/cache/objects/311/l2h/img31.png) VAN DAELE, A., The Haar measure on finite quantum groups, Proc. A.M.S. 125 (1997), 3489-3500. VAN DAELE, A., The Haar measure on finite quantum groups, Proc. A.M.S. 125 (1997), 3489-3500.
![$[29]$ $[29]$](http://images.physicslibrary.org/cache/objects/311/l2h/img32.png) VAN DAELE, A., WANG, S., Universal Quantum Groups, Int. J. of Math. (1996), 255-263. VAN DAELE, A., WANG, S., Universal Quantum Groups, Int. J. of Math. (1996), 255-263. ![$[30]$ $[30]$](http://images.physicslibrary.org/cache/objects/311/l2h/img33.png) WANG, S., Krein Duality for Compact Quantum Groups, J. Math. Phys. 38 (1997), 524-534. WANG, S., Krein Duality for Compact Quantum Groups, J. Math. Phys. 38 (1997), 524-534.
31. WORONOWICZ, S.L., Twisted 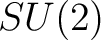 group. An example of non-commutative differential calculus. Publ. RIMS Kyoto Univ. 23 No. 1 (1987), 117-181. group. An example of non-commutative differential calculus. Publ. RIMS Kyoto Univ. 23 No. 1 (1987), 117-181.
![$[32]$ $[32]$](http://images.physicslibrary.org/cache/objects/311/l2h/img35.png) WORONOWICZ, S.L., Compact matrix Pseudogroups, Commun. Math. Phys. 111 (1987), 613-665. WORONOWICZ, S.L., Compact matrix Pseudogroups, Commun. Math. Phys. 111 (1987), 613-665.
33. WORONOWICZ, S.L., Tannaka-Krein duality for compact matrix pseudogroups. Twisted 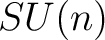 groups, Invent. Math. 93 (1988) 35-76. groups, Invent. Math. 93 (1988) 35-76. ![$[34]$ $[34]$](http://images.physicslibrary.org/cache/objects/311/l2h/img37.png) WORONOWICZ, S.L., A remark on Compact Matrix Quantum Groups, Lett. Math. Phys. 21 (1991), 35-39. WORONOWICZ, S.L., A remark on Compact Matrix Quantum Groups, Lett. Math. Phys. 21 (1991), 35-39. ![$[35]$ $[35]$](http://images.physicslibrary.org/cache/objects/311/l2h/img38.png) WORONOWICZ, S.L., Compact Quantum Groups, Preprint University ofWarszawa (1992). To appear. WORONOWICZ, S.L., Compact Quantum Groups, Preprint University ofWarszawa (1992). To appear.
36. MAES, A. and VanDAELE, A. 1998. Notes on Compact Quantum Groups.,
 , 43 pp. , 43 pp.
|

