|
Capacitors in networks cannot always be grouped into simple series or parallel combinations. As an example, the figure shows three capacitors  , , 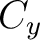 , and , and 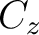 in a delta network, so called because of its triangular shape. This network has three terminals in a delta network, so called because of its triangular shape. This network has three terminals 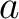 , , 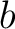 , and , and 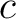 and hence cannot be transformed into a sinle equivalent capacitor. and hence cannot be transformed into a sinle equivalent capacitor.
Figure: The delta network
|
|
It can be shown that as far as any effect on the external circuit is concerned, a delta network is equivalent to what is called a Y network. The name "Y network" also refers to the shape of the network.
I am going to show that the transformation equations that give 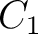 , , 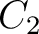 , and , and  in terms of in terms of  , ,  , and , and 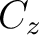 are are
The potential difference 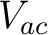 must be the same in both circuits, as must be the same in both circuits, as 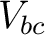 must be. Also, the charge must be. Also, the charge 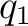 that flows from point that flows from point 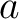 along the wire as indicated must be the same in both circuits, as must along the wire as indicated must be the same in both circuits, as must 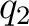 . Now, let us first work with the delta circuit. Suppose the charge flowing through . Now, let us first work with the delta circuit. Suppose the charge flowing through  is is  and to the right. According to Kirchoff's first rule: and to the right. According to Kirchoff's first rule:
Lets play with the equation a little bit..
From Kirchoff's second law:
 Therefore we get the equation:
Therefore we get the equation:
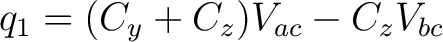 |
(1) |
Similarly, we apply the rule to the right part of the circuit:
We then get the second equation
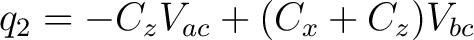 |
(2) |
Solving (1) and (2) simultaneously for 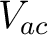 and and  , we get:
Keeping these in mind, we proceed to the Y network. Let us apply Kirchoff's second law to the left part:
From conservation of charge, , we get:
Keeping these in mind, we proceed to the Y network. Let us apply Kirchoff's second law to the left part:
From conservation of charge,
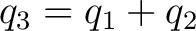 Simplifying the above equation yields:
Similarly for the right part:
The coefficients of corresponding charges in corresponding equations must be the same for both networks. i.e. we compare the equations for Simplifying the above equation yields:
Similarly for the right part:
The coefficients of corresponding charges in corresponding equations must be the same for both networks. i.e. we compare the equations for 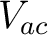 and and 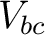 for both networks. Immediately by comparing the coefficient of for both networks. Immediately by comparing the coefficient of 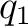 in in 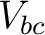 we get:
Now compare the coefficient of we get:
Now compare the coefficient of  :
Substitute the expression we got for :
Substitute the expression we got for 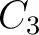 , and solve for , and solve for  to get:
Now we look at the coeffcient of to get:
Now we look at the coeffcient of  in the equation for in the equation for 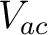 :
Again substituting the expression for :
Again substituting the expression for 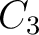 and solving for and solving for 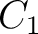 we get:
We have derived the required transformation equations mentioned at the top. we get:
We have derived the required transformation equations mentioned at the top.
|

