 -finite Borel and Radon measures -finite Borel and Radon measures
|
(Topic)
|
|
Let us recall the following data related to Borel space and measure theory:
- sigma–algebra, or
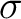 -algebra; -algebra;
- the Borel algebra which is defined as the smallest
 -algebra on the field of real numbers -algebra on the field of real numbers
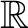 generated by the open intervals of generated by the open intervals of
 ; ;
- Borel space
- Consider a locally compact Hausdorff space
 ; a Borel measure is then defined as any measure ; a Borel measure is then defined as any measure  on the sigma-algebra of Borel sets, that is, the Borel on the sigma-algebra of Borel sets, that is, the Borel  -algebra -algebra
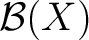 defined on a locally compact Hausdorff space defined on a locally compact Hausdorff space 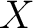 ; ;
- When the Borel measure
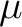 is both inner and outer regular on all Borel sets, it is called a regular Borel measure; is both inner and outer regular on all Borel sets, it is called a regular Borel measure;
- Recall that a topological space
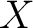 is is 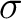 -compact if there exists a sequence -compact if there exists a sequence
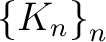 of compact subsets of compact subsets 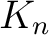 of of 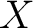 such that : such that :
Definition 0.1 Let
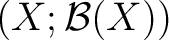 be a Borel space (with the 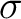 -algebra
 of Borel sets of a topological space  ), and let 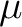 be a measure on the space 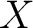 . Then, such a measure is called a 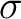 –finite (Borel) measure –finite (Borel) measure if there exists a sequence
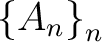 with
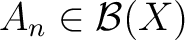 for all 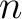 , such that
and also
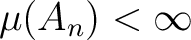 for all 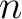 , (ref. [ 1]).
Definition 0.2 If  is an inner regular and locally finite measure, then 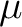 is said to be a Radon measure.
Note Any Borel measure on 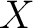 which is finite on such compact subsets is also (Borel) which is finite on such compact subsets is also (Borel) 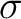 -finite in the above defined sense (Definition 0.1). -finite in the above defined sense (Definition 0.1).
- 1
- M.R. Buneci. 2006., Groupoid C*-Algebras., Surveys in Mathematics and its Applications, Volume 1: 71–98.
- 2
- J.D. Pryce (1973). Basic methods of functional analysis., Hutchinson University Library. Hutchinson, p. 212–217.
- 3
- Alan J. Weir (1974). General integration and measure. Cambridge University Press, pp. 150-184.
- 4
- Boris Hasselblatt, A. B. Katok, Eds. (2002). Handbook of Dynamical Systems., vol. 1A, p.678. North-Holland. on line
|
" -finite Borel and Radon measures" is owned by bci1. -finite Borel and Radon measures" is owned by bci1.
|
|
| Also defines: |
 -finite Borel measure, Radon measure -finite Borel measure, Radon measure |
| Keywords: |
 -finite Borel and Radon measures -finite Borel and Radon measures |
Cross-references: topological, regular, Borel sets, sigma-algebra of Borel sets, locally compact Hausdorff space, field, Borel space
This is version 1 of  -finite Borel and Radon measures, born on 2009-01-17. -finite Borel and Radon measures, born on 2009-01-17.
Object id is 406, canonical name is SigmaFiniteBorelAndRadonMeasures.
Accessed 2135 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

