|
locally compact Hausdorff spaces
|
(Topic)
|
|
Definition 1.1 A locally compact Hausdorff space  is a locally compact topological space
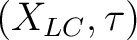 with 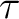 being a Hausdorff topology, that is, if given any distinct points
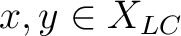 , there exist disjoint sets
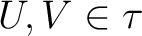 such that,
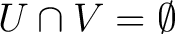 (that is, open sets), and with 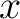 and 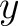 satisfying the conditions that 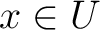 and 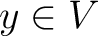 .
- 1
- K.A. Hardie, K.H. Kamps and R.W. Kieboom., A homotopy 2-groupoid of a Hausdorff space, Applied Cat. Structures, 8 (2000): 209-234.
- 2
- R. Brown, K.A. Hardie, K.H. Kamps and T. Porter, A homotopy double groupoid of a Hausdorff space, Theory and Applications of Categories 10,(2002): 71-93.
|
"locally compact Hausdorff spaces" is owned by bci1.
|
|
| Keywords: |
locally compact Hausdorff spaces |
Cross-references: algebraic topology, 2-groupoid, homotopy, QG, quantum gravity, QCG, axiomatic QFT, AQFT, algebraic, TQFT, QFT, QAT, quantum algebraic topology, representations, quantum groupoid, extended quantum symmetries, groupoid, topological, concept
There are 7 references to this object.
This is version 1 of locally compact Hausdorff spaces, born on 2009-03-15.
Object id is 597, canonical name is LocallyCompactHausdorffSpaces.
Accessed 1284 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

