|
functor category
|
(Definition)
|
|
Definition 0.1 In order to define the concept of functor category, let us consider for any two categories
 and
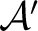 , the class
of all covariant functors from
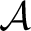 to
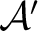 . For any two such functors
![$F, K \in [\mathcal{\mathcal A}, \mathcal{\mathcal A'}]$ $F, K \in [\mathcal{\mathcal A}, \mathcal{\mathcal A'}]$](http://images.physicslibrary.org/cache/objects/603/l2h/img6.png) ,
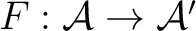 and
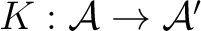 , let us denote the class of all natural transformations from 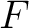 to 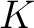 by ![$[F, K]$ $[F, K]$](http://images.physicslibrary.org/cache/objects/603/l2h/img11.png) . In the particular case when ![$[F, K]$ $[F, K]$](http://images.physicslibrary.org/cache/objects/603/l2h/img12.png) is a set one can still define for a small category
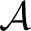 , the set
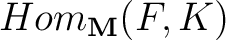 . Thus, cf. p. 62 in [ 1], when
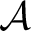 is a small category the `class' ![$[F, K]$ $[F, K]$](http://images.physicslibrary.org/cache/objects/603/l2h/img16.png) of natural transformations from  to 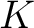 may be viewed as a subclass of the cartesian product
![$\prod_{A \in \mathcal{\mathcal A}}[F(A), K(A)]$ $\prod_{A \in \mathcal{\mathcal A}}[F(A), K(A)]$](http://images.physicslibrary.org/cache/objects/603/l2h/img19.png) , and because the latter is a set so is ![$[F, K]$ $[F, K]$](http://images.physicslibrary.org/cache/objects/603/l2h/img20.png) as well. Therefore, with the categorical law of composition of natural transformations of functors, and for
 being small,
![$\textbf{M} = [\mathcal{\mathcal A},\mathcal{\mathcal A'}]$ $\textbf{M} = [\mathcal{\mathcal A},\mathcal{\mathcal A'}]$](http://images.physicslibrary.org/cache/objects/603/l2h/img22.png) satisfies the conditions for the definition of a category satisfies the conditions for the definition of a category, and it is in fact a functor category.
Remark: In the general case when
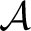 is not small, the proper class is not small, the proper class
![$\textbf{M} = [\mathcal{\mathcal A}, \mathcal{\mathcal A'}]$ $\textbf{M} = [\mathcal{\mathcal A}, \mathcal{\mathcal A'}]$](http://images.physicslibrary.org/cache/objects/603/l2h/img24.png) may be endowed with the structure of a supercategory (defined as any formal interpretation of ETAS) with the usual categorical composition law for natural transformations of functors. Similarly, one can construct a meta-category defined as the supercategory of all functor categories. may be endowed with the structure of a supercategory (defined as any formal interpretation of ETAS) with the usual categorical composition law for natural transformations of functors. Similarly, one can construct a meta-category defined as the supercategory of all functor categories.
- 1
- Mitchell, B.: 1965, Theory of Categories, Academic Press: London.
- 2
- Refs.
![$[15],[17],[18]$ $[15],[17],[18]$](http://images.physicslibrary.org/cache/objects/603/l2h/img25.png) and and ![$[288]$ $[288]$](http://images.physicslibrary.org/cache/objects/603/l2h/img26.png) in the Bibliography of Category Theory and Algebraic Topology. Categories, Functors and Automata Theory: A Novel Approach to Quantum Automata through Algebraic-Topological Quantum Computations., Proceed. 4th Intl. Congress LMPS, P. Suppes, Editor (August-Sept. 1971). in the Bibliography of Category Theory and Algebraic Topology. Categories, Functors and Automata Theory: A Novel Approach to Quantum Automata through Algebraic-Topological Quantum Computations., Proceed. 4th Intl. Congress LMPS, P. Suppes, Editor (August-Sept. 1971).
|
"functor category" is owned by bci1.
|
|
See Also: category, categorical diagrams defined as functors, category theory, algebraic topology
| Keywords: |
functor, category, functor category |
Cross-references: composition law, ETAS, supercategory, composition, small category, natural transformations, categories, concept
There are 9 references to this object.
This is version 5 of functor category, born on 2009-03-19, modified 2009-04-06.
Object id is 603, canonical name is FunctorCategories.
Accessed 2478 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

