|
Some examples of applying the Einstein summation notation.
Example 1. Let us consider the quantity
for a three dimensional space. Since the index  occurs as both a subscript and a superscript, we sum on occurs as both a subscript and a superscript, we sum on  from 1 to 3. This yields from 1 to 3. This yields
Now each term of 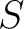 is such that is such that 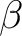 is both a subscript and superscript. Summing on is both a subscript and superscript. Summing on  from 1 to 3 as prescribed by our summation convention yields the quadratic form from 1 to 3 as prescribed by our summation convention yields the quadratic form
Example 2. If
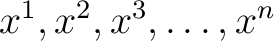 is a set of independent variables, then is a set of independent variables, then
and if 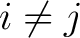
We may write
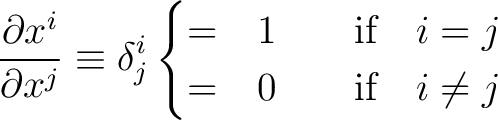 |
(1) |
The symbol
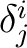 is called the Kronecker delta. We have is called the Kronecker delta. We have
Let us now assume that the quadratic form at the end of example 1 vanishes identically for all values of the independent variables  , ,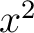 , , 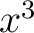 , and , and 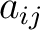 to be constant. Differentiating to be constant. Differentiating
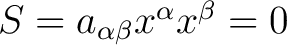 with respect to a given variable, say with respect to a given variable, say 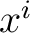 , yields , yields
Now differentiating with respect to 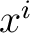 yields yields
so that
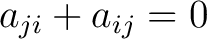 or or
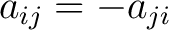 for for
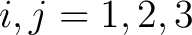 . .
Example 3. We define
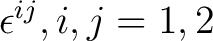 , to have the following numerical values: Let , to have the following numerical values: Let
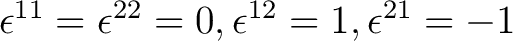 . We now consider the expression . We now consider the expression
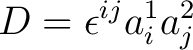 |
(2) |
Expanding (2) by use of our summation convention yields
The reader who is familiar with second-order determinants quickly recognizes that
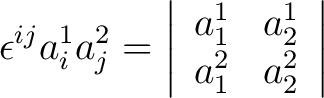 |
(3) |
Example 4. The system of equations
 |
(4) |
represents a coordinate transformation from an
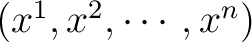 coordinate system to a coordinate system to a
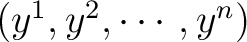 coordinate system. From the calculus we have coordinate system. From the calculus we have
The 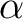 in the term in the term
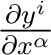 is to be considered as a subscript. If, furthermore, the is to be considered as a subscript. If, furthermore, the 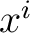 , ,
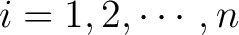 , can be solved for the , can be solved for the
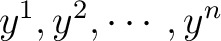 , and assuming differentiability of the , and assuming differentiability of the 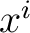 with respect to each with respect to each 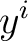 , one obtains , one obtains
Differentiating this expression with respect to 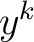 yields yields
Multiplying both sides of this equation by
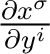 amd summing on the inex amd summing on the inex  yields yields
or
which yields
In particular, if 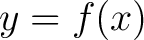 , then , then
[1] Lass, Harry. "Elements of pure and applied mathematics" New York: McGraw-Hill Companies, 1957.
This entry is a derivative of the Public domain work [1].
| 
