![[parent]](https://images.physicslibrary.org/images/uparrow.png) derivation of heat equation
derivation of heat equation
|
(Derivation)
|
|
|
Let us consider the heat conduction in a homogeneous matter with density  and specific heat capacity and specific heat capacity  . Denote by . Denote by
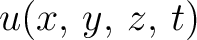 the temperature in the point the temperature in the point
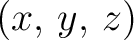 at the time at the time  . Let . Let 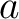 be a simple closed surface in the matter and be a simple closed surface in the matter and  the spatial region restricted by it. the spatial region restricted by it.
When the growth of the temperature of a volume element 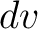 in the time in the time 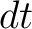 is is 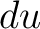 , the element releases the amount , the element releases the amount
of heat, which is the heat flux through the surface of 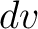 . Thus if there are no sources and sinks of heat in . Thus if there are no sources and sinks of heat in 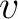 , the heat flux through the surface , the heat flux through the surface 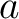 in in 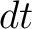 is is
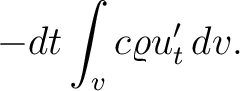 |
(1) |
On the other hand, the flux through 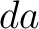 in the time in the time  must be proportional to must be proportional to 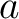 , to , to 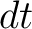 and to the derivative of the temperature in the direction of the normal line of the surface element and to the derivative of the temperature in the direction of the normal line of the surface element 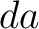 , i.e. the flux is
where , i.e. the flux is
where 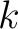 is a positive constant (because the heat flows always from higher temperature to lower one). Consequently, the heat flux through the whole surface is a positive constant (because the heat flows always from higher temperature to lower one). Consequently, the heat flux through the whole surface 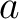 is
which is, by the Gauss's theorem, same as is
which is, by the Gauss's theorem, same as
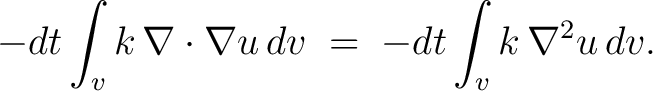 |
(2) |
Equating the expressions (1) and (2) and dividing by 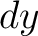 , one obtains
Since this equation is valid for any region , one obtains
Since this equation is valid for any region 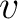 in the matter, we infer that
Denoting in the matter, we infer that
Denoting
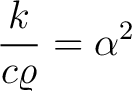 , we can write this equation as , we can write this equation as
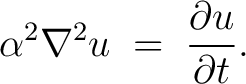 |
(3) |
This is the differential equation of heat conduction, first derived by Fourier.
|
"derivation of heat equation" is owned by pahio.
|
|
See Also: derivation of wave equation
This object's parent.
Cross-references: differential equation, theorem, flux, volume, temperature, conduction, heat
This is version 1 of derivation of heat equation, born on 2009-01-20.
Object id is 417, canonical name is DerivationOfHeatEquation.
Accessed 1115 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

