Definition 1.1 An algebroid structure  will be specifically defined to mean either a ring, or more generally, any of the specifically defined algebras, but with several objects instead of a single object, in the sense specified by Mitchell (1965). Thus, an algebroid has been defined (Mosa, 1986a; Brown and Mosa 1986b, 2008) as follows. An 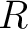 -algebroid -algebroid 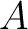 on a set
of “objects" 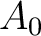 is a directed graph over 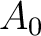 such that for each
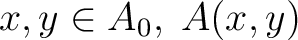 has an 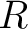 -module structure and there is an 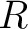 -bilinear function
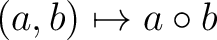 called “ composition" and satisfying the associativity condition, and the existence of identities.
Definition 1.2 A pre-algebroid has the same structure as an algebroid and the same axioms except for the fact that the existence of identities
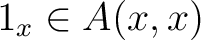 is not assumed. For example, if 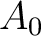 has exactly one object, then an  -algebroid 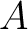 over 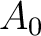 is just an 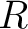 -algebra. An ideal in 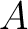 is then an example of a pre-algebroid.
Let 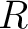 be a commutative ring. be a commutative ring.
An 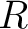 -category -category
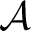 is a category equipped with an is a category equipped with an  -module structure on each hom set such that the composition is -module structure on each hom set such that the composition is 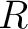 -bilinear. More precisely, let us assume for instance that we are given a commutative ring -bilinear. More precisely, let us assume for instance that we are given a commutative ring 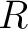 with identity. Then a small with identity. Then a small  -category–or equivalently an -category–or equivalently an 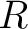 -algebroid– will be defined as a category enriched in the monoidal category of -algebroid– will be defined as a category enriched in the monoidal category of 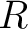 -modules, with respect to the monoidal structure of tensor product. This means simply that for all objects -modules, with respect to the monoidal structure of tensor product. This means simply that for all objects 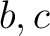 of of
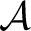 , the set , the set
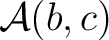 is given the structure of an is given the structure of an  -module, and composition -module, and composition
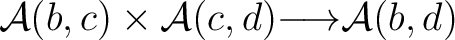 is is 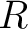 –bilinear, or is a morphism of –bilinear, or is a morphism of 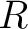 -modules -modules
 . .
If
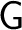 is a groupoid (or, more generally, a category) then we can construct an is a groupoid (or, more generally, a category) then we can construct an 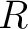 -algebroid -algebroid
 as follows. The object set of as follows. The object set of
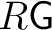 is the same as that of is the same as that of
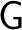 and and
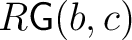 is the free is the free 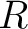 -module on the set -module on the set
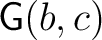 , with composition given by the usual bilinear rule, extending the composition of , with composition given by the usual bilinear rule, extending the composition of
 . .
Alternatively, one can define
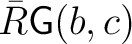 to be the set of functions to be the set of functions
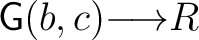 with finite support, and then we define the convolution product as follows: with finite support, and then we define the convolution product as follows:
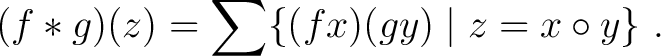 |
(1.1) |
As it is very well known, only the second construction is natural for the topological case, when one needs to replace `function' by `continuous function with compact support' (or locally compact support for the QFT extended symmetry sectors), and in this case
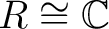 . The point made here is that to carry out the usual construction and end up with only an algebra rather than an algebroid, is a procedure analogous to replacing a groupoid . The point made here is that to carry out the usual construction and end up with only an algebra rather than an algebroid, is a procedure analogous to replacing a groupoid
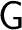 by a semigroup by a semigroup
 in which the compositions not defined in in which the compositions not defined in 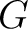 are defined to be 0 in are defined to be 0 in 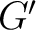 . We argue that this construction removes the main advantage of groupoids, namely the spatial component given by the set of objects. . We argue that this construction removes the main advantage of groupoids, namely the spatial component given by the set of objects.
Remarks: One can also define categories of algebroids, 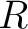 -algebroids, double algebroids , and so on. A `category' of -algebroids, double algebroids , and so on. A `category' of 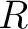 -categories is however a super-category -categories is however a super-category 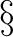 , or it can also be viewed as a specific example of a metacategory (or , or it can also be viewed as a specific example of a metacategory (or 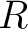 -supercategory, in the more
general case of multiple operations–categorical `composition laws' being defined within the same structure, for the same class, -supercategory, in the more
general case of multiple operations–categorical `composition laws' being defined within the same structure, for the same class,  ). ).
| 
