|
Let 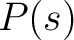 and and 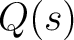 be polynomials with the degree of the former less than the degree of the latter. be polynomials with the degree of the former less than the degree of the latter.
- If all complex zeroes
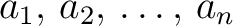 of of 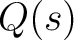 are simple, then are simple, then
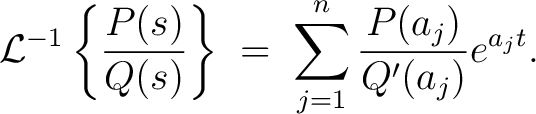 |
(1) |
- If the different zeroes
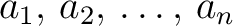 of of 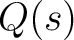 have the multiplicities have the multiplicities
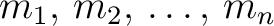 , respectively, we denote , respectively, we denote
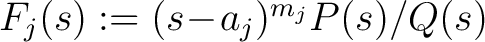 ; then ; then
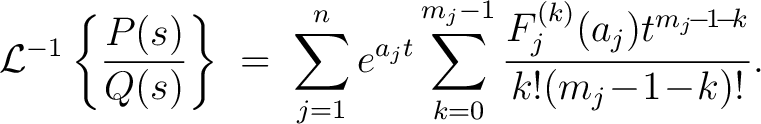 |
(2) |
A special case of the Heaviside formula (1) is
Example. Since the zeros of the binomial
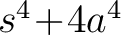 are are
 , we obtain , we obtain
Proof of (1). Without hurting the generality, we can suppose that 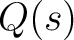 is monic. Therefore is monic. Therefore
For
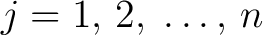 , denoting
one has , denoting
one has
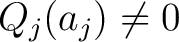 . We have a partial fraction expansion of the form . We have a partial fraction expansion of the form
 |
(3) |
with constants 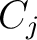 . According to the linearity and the formula 1 of the parent entry, one gets . According to the linearity and the formula 1 of the parent entry, one gets
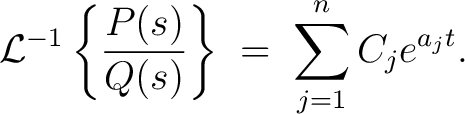 |
(4) |
For determining the constants 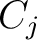 , multiply (3) by , multiply (3) by 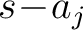 . It yields
Setting to this identity . It yields
Setting to this identity 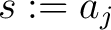 gives the value gives the value
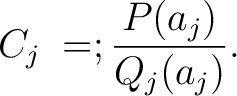 |
(5) |
But since
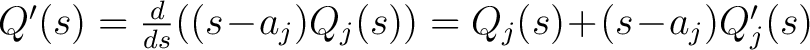 , we see that , we see that
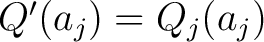 ; thus the equation (5) may be written ; thus the equation (5) may be written
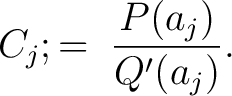 |
(6) |
The values (6) in (4) produce the formula (1).
- 1
- K. V¨AISÄLÄ: Laplace-muunnos. Handout Nr. 163. Teknillisen korkeakoulun ylioppilaskunta, Otaniemi, Finland (1968).
|

