This is a topic entry that introduces quantum operator algebras and presents concisely the important roles they play in quantum field theories.
Definition 0.1 Quantum operator algebras (QOA) in quantum field theories are defined as the algebras of observable operators, and as such, they are also related to the von Neumann algebra; quantum operators are usually defined on Hilbert spaces, or in some QFTs on Hilbert space bundles or other similar families of spaces.
Remark 0.1 representations of Banach  -algebras -algebras– that are defined on Hilbert spaces– are closely related to C* -algebra representations which provide a useful approach to defining quantum space-times.
Important examples of quantum operators are: the Hamiltonian operator (or Schrödinger operator), the position and momentum operators, Casimir operators, unitary operators and spin operators. The observable operators are also self-adjoint. More general operators were recently defined, such as Prigogine's superoperators.
Another development in quantum theories was the introduction of Frechét nuclear spaces or `rigged' Hilbert spaces (Hilbert space bundles). The following sections define several types of quantum operator algebras that provide the foundation of modern quantum field theories in mathematical physics.
Quantum theories adopted a new lease of life post 1955 when von Neumann beautifully re-formulated quantum mechanics (QM) and quantum theories (QT) in the mathematically rigorous context of Hilbert spaces and operator algebras defined over such spaces. From a current physics perspective, von Neumann' s approach to quantum mechanics has however done much more: it has not only paved the way to expanding the role of symmetry in physics, as for example with the Wigner-Eckhart theorem and its applications, but also revealed the fundamental importance in quantum physics of the state space geometry of quantum operator algebras.
Let 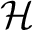 denote a complex (separable) Hilbert space. A von Neumann algebra denote a complex (separable) Hilbert space. A von Neumann algebra
 acting on acting on 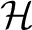 is a subset of the algebra of all bounded operators is a subset of the algebra of all bounded operators
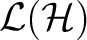 such that: such that:
- (i)
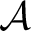 is closed under the adjoint operation (with the adjoint of an element is closed under the adjoint operation (with the adjoint of an element 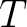 denoted by denoted by 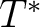 ). ).
- (ii)
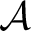 equals its bicommutant, namely: equals its bicommutant, namely:
 |
(0.1) |
If one calls a commutant of a set
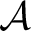 the special set of bounded operators on the special set of bounded operators on
 which commute with all elements in which commute with all elements in
 , then this second condition implies that the commutant of the commutant of , then this second condition implies that the commutant of the commutant of
 is again the set is again the set
 . .
On the other hand, a von Neumann algebra
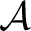 inherits a unital subalgebra from inherits a unital subalgebra from
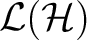 , and according to the first condition in its definition , and according to the first condition in its definition
 , it does indeed inherit a , it does indeed inherit a  -subalgebra structure as further explained in the next section on C* -algebras. Furthermore, one also has available a notable `bicommutant theorem' which states that: “ -subalgebra structure as further explained in the next section on C* -algebras. Furthermore, one also has available a notable `bicommutant theorem' which states that: “
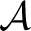 is a von Neumann algebra if and only if is a von Neumann algebra if and only if
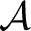 is a is a  -subalgebra of -subalgebra of
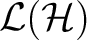 , closed for the smallest topology defined by continuous maps , closed for the smallest topology defined by continuous maps
 for all for all
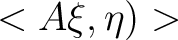 where where  denotes the inner product defined on denotes the inner product defined on 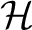 ”. ”.
For a well-presented treatment of the geometry of the state spaces of quantum operator algebras, the reader is referred to Aflsen and Schultz (2003; []).
First, a unital associative algebra consists of a linear space 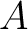 together with two linear maps:
satisfying the conditions
This first condition can be seen in terms of a commuting diagram : together with two linear maps:
satisfying the conditions
This first condition can be seen in terms of a commuting diagram :
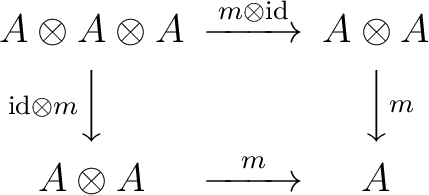 |
(0.4) |
Next suppose we consider `reversing the arrows', and take an algebra 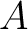 equipped with a linear homorphisms equipped with a linear homorphisms
 , satisfying, for , satisfying, for  : :
We call 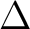 a comultiplication, which is said to be coasociative in so far that the following diagram commutes a comultiplication, which is said to be coasociative in so far that the following diagram commutes
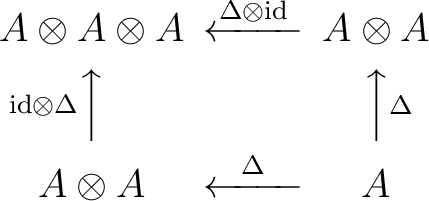 |
(0.6) |
There is also a counterpart to 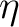 , the counity map , the counity map
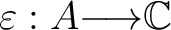 satisfying satisfying
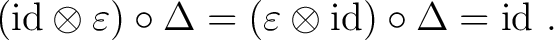 |
(0.7) |
A bialgebra
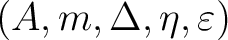 is a linear space is a linear space 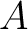 with maps with maps
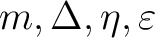 satisfying the above properties. satisfying the above properties.
Now to recover anything resembling a group structure, we must append such a bialgebra with an antihomomorphism
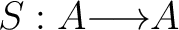 , satisfying , satisfying
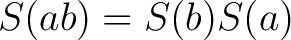 , for , for 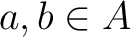 . This map is defined implicitly via the property : . This map is defined implicitly via the property :
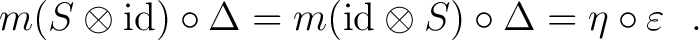 |
(0.8) |
We call  the antipode map. the antipode map.
A Hopf algebra is then a bialgebra
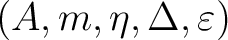 equipped with an antipode map equipped with an antipode map 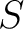 . .
Commutative and non-commutative Hopf algebras form the backbone of quantum `groups' and are essential to the generalizations of symmetry. Indeed, in most respects a quantum `group' is closely related to its dual Hopf algebra; in the case of a finite, commutative quantum group its dual Hopf algebra is obtained via Fourier transformation of the group elements. When Hopf algebras are actually associated with their dual, proper groups of matrices, there is considerable scope for their representations on both finite and infinite dimensional Hilbert spaces.
Recall that a groupoid
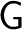 is, loosely speaking, a small category with inverses over its set of objects is, loosely speaking, a small category with inverses over its set of objects
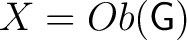 . One often writes . One often writes
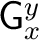 for the set of morphisms in for the set of morphisms in
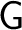 from from  to to  . A topological groupoid consists of a space . A topological groupoid consists of a space
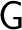 , a distinguished subspace , a distinguished subspace
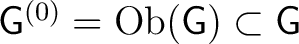 , called the space of objects of , called the space of objects of
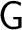 , together with maps , together with maps
![$\displaystyle r,s~:~ \xymatrix{ {\mathsf{G}}\ar@<1ex>[r]^r \ar[r]_s & {\mathsf{G}}^{(0)} }$ $\displaystyle r,s~:~ \xymatrix{ {\mathsf{G}}\ar@<1ex>[r]^r \ar[r]_s & {\mathsf{G}}^{(0)} }$](http://images.physicslibrary.org/cache/objects/571/l2h/img60.png) |
(0.9) |
called the range and source maps respectively, together with a law of composition
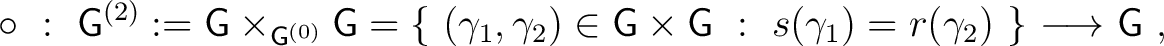 |
(0.10) |
such that the following hold :
- (1)
-
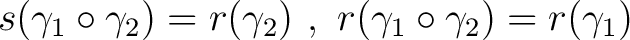 , for all , for all
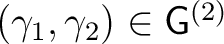 . .
- (2)
-
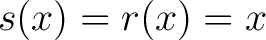 , for all , for all
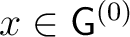 . .
- (3)
-
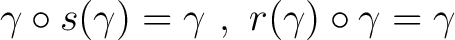 , for all , for all
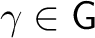 . .
- (4)
-
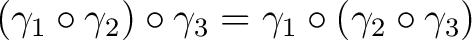 . .
- (5)
- Each
 has a two–sided inverse has a two–sided inverse
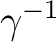 with with
 . Furthermore, only for topological groupoids the inverse map needs be continuous. It is usual to call . Furthermore, only for topological groupoids the inverse map needs be continuous. It is usual to call
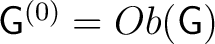 the set of objects of the set of objects of
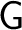 . For . For
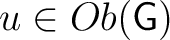 , the set of arrows , the set of arrows
 forms a group forms a group
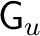 , called the isotropy group of , called the isotropy group of
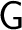 at at 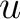 . .
Thus, as it is well kown, a topological groupoid is just a groupoid internal to the category of topological spaces and continuous maps. The notion of internal groupoid has proved significant in a number of fields, since groupoids generalise bundles of groups, group actions, and equivalence relations. For a further study of groupoids we refer the reader to Brown (2006).
Several examples of groupoids are:
- (a) locally compact groups, transformation groups , and any group in general (e.g. [59]
- (b) equivalence relations
- (c) tangent bundles
- (d) the tangent groupoid
- (e) holonomy groupoids for foliations
- (f) Poisson groupoids
- (g) graph groupoids.
As a simple, helpful example of a groupoid, consider (b) above. Thus, let R be an equivalence relationhttp://physicslibrary.org/encyclopedia/Bijective.html on a set X. Then R is a groupoid under the following operations:
 . Here, . Here,
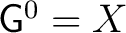 , (the diagonal of , (the diagonal of
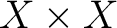 ) and ) and
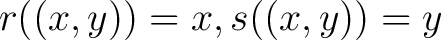 . .
Therefore,  = =
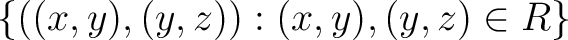 . When . When
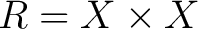 , R is called a trivial groupoid. A special case of a trivial groupoid is , R is called a trivial groupoid. A special case of a trivial groupoid is
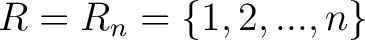 
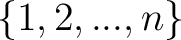 . (So every i is equivalent to every j). Identify . (So every i is equivalent to every j). Identify
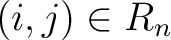 with the matrix unit with the matrix unit 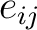 . Then the groupoid . Then the groupoid 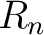 is just matrix multiplication except that we only multiply is just matrix multiplication except that we only multiply
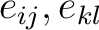 when when 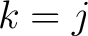 , and , and
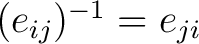 . We do not really lose anything by restricting the multiplication, since the pairs . We do not really lose anything by restricting the multiplication, since the pairs
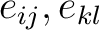 excluded from groupoid multiplication just give the 0 product in normal algebra anyway. For a groupoid excluded from groupoid multiplication just give the 0 product in normal algebra anyway. For a groupoid
 to be a locally compact groupoid means that to be a locally compact groupoid means that
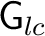 is required to be a (second countable) locally compact Hausdorff space, and the product and also inversion maps are required to be continuous. Each is required to be a (second countable) locally compact Hausdorff space, and the product and also inversion maps are required to be continuous. Each
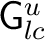 as well as the unit space as well as the unit space
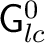 is closed in is closed in
 . What replaces the left Haar measure on . What replaces the left Haar measure on
 is a system of measures is a system of measures 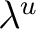 ( (
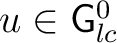 ), where ), where 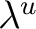 is a positive regular Borel measure on is a positive regular Borel measure on
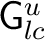 with dense support. In addition, the with dense support. In addition, the
 's are required to vary continuously (when integrated against 's are required to vary continuously (when integrated against
 and to form an invariant family in the sense that for each x, the map and to form an invariant family in the sense that for each x, the map
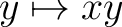 is a measure preserving homeomorphism from is a measure preserving homeomorphism from
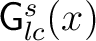 onto onto
 . Such a system . Such a system
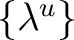 is called a left Haar system for the locally compact groupoid is called a left Haar system for the locally compact groupoid
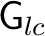 . .
This is defined more precisely in the next subsection.
Let
![$\displaystyle \xymatrix{ {\mathsf{G}}\ar@<1ex>[r]^r \ar[r]_s & {\mathsf{G}}^{(0)}}=X$ $\displaystyle \xymatrix{ {\mathsf{G}}\ar@<1ex>[r]^r \ar[r]_s & {\mathsf{G}}^{(0)}}=X$](http://images.physicslibrary.org/cache/objects/571/l2h/img113.png) |
(0.11) |
be a locally compact, locally trivial topological groupoid with its transposition into transitive (connected) components. Recall that for 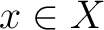 , the costar of , the costar of 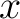 denoted denoted
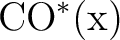 is defined as the closed set is defined as the closed set
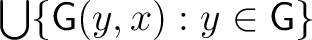 , whereby , whereby
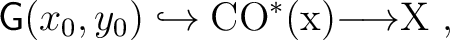 |
(0.12) |
is a principal
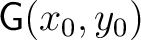 –bundle relative to fixed base points –bundle relative to fixed base points
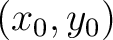 . Assuming all relevant sets are locally compact, then following Seda (1976), a (left) Haar system on . Assuming all relevant sets are locally compact, then following Seda (1976), a (left) Haar system on
 denoted denoted
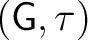 (for later purposes), is defined to comprise of i) a measure (for later purposes), is defined to comprise of i) a measure  on on
 , ii) a measure , ii) a measure 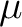 on on 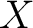 and iii) a measure and iii) a measure 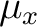 on on
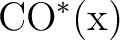 such that for every Baire set such that for every Baire set  of of
 , the following hold on setting , the following hold on setting
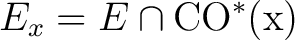 : :
| (1) |
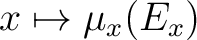 is measurable. is measurable. |
| (2) |
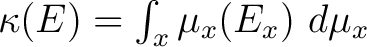 . . |
| (3) |
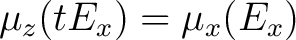 , for all , for all
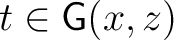 and and
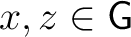 . . |
The presence of a left Haar system on
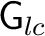 has important topological implications: it requires that the range map has important topological implications: it requires that the range map
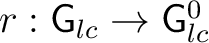 is open. For such a is open. For such a
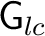 with a left Haar system, the vector space with a left Haar system, the vector space
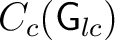 is a convolution *–algebra, where for is a convolution *–algebra, where for
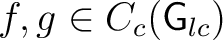 : :
with
One has
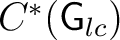 to be the enveloping C*–algebra of to be the enveloping C*–algebra of
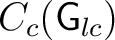 (and also representations are required to be continuous in the inductive limit topology). Equivalently, it is the completion of (and also representations are required to be continuous in the inductive limit topology). Equivalently, it is the completion of
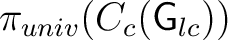 where where
 is the universal representation of is the universal representation of
 . For example, if . For example, if
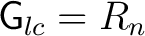 , then , then
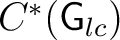 is just the finite dimensional algebra is just the finite dimensional algebra
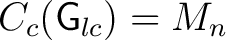 , the span of the , the span of the 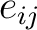 's. 's.
There exists a measurable Hilbert bundlehttp://physicslibrary.org/encyclopedia/HilbertBundle.html
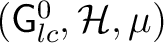 with with
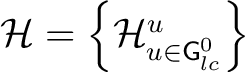 and a G-representation L on and a G-representation L on  . Then, for every pair . Then, for every pair  of square integrable sections of of square integrable sections of  , it is required that the function , it is required that the function
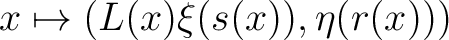 be be 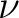 –measurable. The representation –measurable. The representation 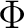 of of
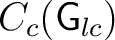 is then given by: is then given by:
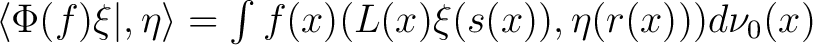 . .
The triple
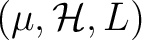 is called a measurable is called a measurable
 –Hilbert bundle. –Hilbert bundle.
- 1
- E. M. Alfsen and F. W. Schultz: Geometry of State Spaces of Operator Algebras, Birkh'́auser, Boston–Basel–Berlin (2003).
- 2
- I. Baianu : Categories, Functors and Automata Theory: A Novel Approach to Quantum Automata through Algebraic–Topological Quantum Computations., Proceed. 4th Intl. Congress LMPS, (August-Sept. 1971).
- 3
- I.C. Baianu, N. Boden and D. Lightowlers.1981. NMR Spin–Echo Responses of Dipolar–Coupled Spin–1/2 Triads in Solids., J. Magnetic Resonance, 43:101–111.
- 4
- I. C. Baianu, J. F. Glazebrook and R. Brown.: A Non–Abelian, Categorical Ontology of Spacetimes and Quantum Gravity., Axiomathes 17,(3-4): 353-408(2007).
- 5
- F.A. Bais, B. J. Schroers and J. K. Slingerland: Broken quantum symmetry and confinement phases in planar physics, Phys. Rev. Lett. 89 No. 18 (1–4): 181-201 (2002).
- 6
- J.W. Barrett.: Geometrical measurements in three-dimensional quantum gravity. Proceedings of the Tenth Oporto Meeting on Geometry, Topology and Physics (2001). Intl. J. Modern Phys. A 18 , October, suppl., 97-113 (2003)
- 7
- M. Chaician and A. Demichev: Introduction to Quantum Groups, World Scientific (1996).
- 8
- Coleman and De Luccia: Gravitational effects on and of vacuum decay., Phys. Rev. D 21: 3305 (1980).
- 9
- A. Connes: Noncommutative Geometry, Academic Press 1994.
- 10
- L. Crane and I.B. Frenkel. Four-dimensional topological quantum field theory, Hopf categories, and the canonical bases. Topology and physics. J. Math. Phys. 35 (no. 10): 5136-5154 (1994).
- 11
- W. Drechsler and P. A. Tuckey: On quantum and parallel transport in a Hilbert bundle over spacetime., Classical and Quantum Gravity, 13:611–632 (1996). doi: 10.1088/0264–9381/13/4/004
- 12
- V. G. Drinfel'd: Quantum groups, In Proc. Int. Cong. of Mathematicians, Berkeley 1986, (ed. A. Gleason), Berkeley, 798–820 (1987).
- 13
- G. J. Ellis: Higher dimensional crossed modules of algebras, J. of Pure Appl. Algebra 52 (1988), 277–282.
- 14
- P.. I. Etingof and A. N. Varchenko, Solutions of the Quantum Dynamical Yang-Baxter Equation and Dynamical Quantum Groups, Comm.Math.Phys., 196: 591-640 (1998)
- 15
- P. I. Etingof and A. N. Varchenko: Exchange dynamical quantum groups, Commun. Math. Phys. 205 (1): 19–52 (1999)
- 16
- P. I. Etingof and O. Schiffmann: Lectures on the dynamical Yang–Baxter equations, in Quantum Groups and Lie Theory (Durham, 1999), pp. 89–129, Cambridge University Press, Cambridge, 2001.
- 17
- B. Fauser: A treatise on quantum Clifford Algebras. Konstanz, Habilitationsschrift.
 (2002). (2002).
- 18
- B. Fauser: Grade Free product Formulae from Grassman–Hopf Gebras. Ch. 18 in R. Ablamowicz, Ed., Clifford Algebras: Applications to Mathematics, Physics and Engineering, Birkhäuser: Boston, Basel and Berlin, (2004).
- 19
- J. M. G. Fell. 1960. “The Dual Spaces of C*–Algebras.”, Transactions of the American Mathematical Society, 94: 365–403 (1960).
- 20
- F.M. Fernandez and E. A. Castro.: (Lie) Algebraic Methods in Quantum Chemistry and Physics., Boca Raton: CRC Press, Inc (1996).
- 21
- R. P. Feynman: Space–Time Approach to Non–Relativistic Quantum Mechanics, Reviews of Modern Physics, 20: 367-387 (1948). [It is also reprinted in (Schwinger 1958).]
- 22
- A. Fröhlich, Non-Abelian Homological Algebra. I. Derived functors and satellites., Proc. London Math. Soc. (3), 11: 239–252 (1961).
- 23
- Gel'fand, I. and Naimark, M., 1943, On the Imbedding of Normed Rings into the Ring of Operators in Hilbert Space, Recueil Mathématique [Matematicheskii Sbornik] Nouvelle Série, 12 [54]: 197-213. [Reprinted in C*-algebras: 1943–1993, in the series Contemporary Mathematics, 167, Providence, R.I. : American Mathematical Society, 1994.]
- 24
- R. Gilmore: “Lie Groups, Lie Algebras and Some of Their Applications.”, Dover Publs., Inc.: Mineola and New York, 2005.
- 25
- P. Hahn: Haar measure for measure groupoids., Trans. Amer. Math. Soc. 242: 1–33(1978).
- 26
- P. Hahn: The regular representations of measure groupoids., Trans. Amer. Math. Soc. 242:34–72(1978).
- 27
- R. Heynman and S. Lifschitz. 1958. Lie Groups and Lie Algebras., New York and London: Nelson Press.
- 28
- C. Heunen, N. P. Landsman, B. Spitters.: A topos for algebraic quantum theory, (2008)
![$arXiv:0709.4364v2 [quant-ph]$ $arXiv:0709.4364v2 [quant-ph]$](http://images.physicslibrary.org/cache/objects/571/l2h/img166.png)
|

