|
|
Definition 0.1 A (classical) automaton, s-automaton
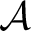 , or sequential machine, is defined as a quintuple of sets, 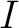 ,  and  , and set-theoretical mappings,
where  is the set of s-automaton inputs, is the set of s-automaton inputs,  is the set of states (or the state space of the s-automaton), is the set of states (or the state space of the s-automaton),  is the set of s-automaton outputs, is the set of s-automaton outputs, 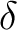 is the transition function that maps an s-automaton state is the transition function that maps an s-automaton state 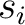 onto its next state onto its next state 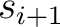 in response to a specific s-automaton input in response to a specific s-automaton input 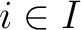 , and , and  is the output function that maps couples of consecutive (or sequential) s-automaton states is the output function that maps couples of consecutive (or sequential) s-automaton states
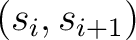 onto s-automaton outputs onto s-automaton outputs 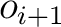 : :
(hence the older name of sequential machine for an s-automaton).
Definition 0.2 A categorical automaton can also be defined by a commutative square diagram containing all of the above components.
With the above automaton definition(s) one can now also define morphisms between automata and their composition.
Definition 0.3 A homomorphism of automata or automata homomorphism is a morphism of automata quintuples that preserves commutativity of the set-theoretical mapping compositions of both the transition function  and the output function 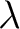 .
With the above two definitions one now has sufficient data to define the category of automata and automata homomorphisms.
Definition 0.4 A category of automata is defined as a category of quintuples
 and automata homomorphisms
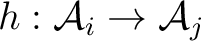 , such that these homomorphisms commute with both the transition and the output functions of any automata
 and
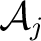 .
Remarks:
- Automata homomorphisms can be considered also as automata transformations or as semigroup homomorphisms, when the state space,
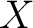 , of the automaton is defined as a semigroup , of the automaton is defined as a semigroup  . .
- Abstract automata have numerous realizations in the real world as : machines, robots, devices, computers, supercomputers, always considered as discrete state space sequential machines.
- Fuzzy or analog devices are not included as standard automata.
- Similarly, variable (transition function) automata are not included, but Universal Turing machines are.
Definition 0.5 An alternative definition of an automaton is also in use: as a five-tuple
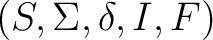 , where 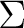 is a non-empty set of symbols 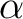 such that one can define a configuration of the automaton as a couple
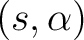 of a state 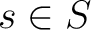 and a symbol
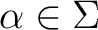 . Then 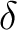 defines a “next-state relation, or a transition relation” which associates to each configuration
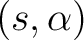 a subset
 of S- the state space of the automaton. With this formal automaton definition, the category of abstract automata can be defined by specifying automata homomorphisms in terms of the morphisms between five-tuples representing such abstract automata.
Example 0.1 A special case of automaton is that of a stable automaton when all its state transitions are reversible; then its state space can be seen to possess a groupoid ( algebraic) structure. The category of reversible automata is then a 2-category, and also a subcategory of the 2-category of groupoids, or the groupoid category.
Definition 0.6 An alternative definition of an automaton is also in use: as a five-tuple
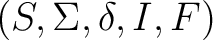 , where 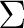 is a non-empty set of symbols 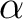 such that one can define a configuration of the automaton as a couple
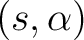 of a state 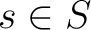 and a symbol
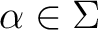 . Then 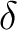 defines a “next-state relation, or a transition relation” which associates to each configuration
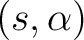 a subset
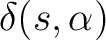 of S- the state space of the automaton. With this formal automaton definition, the category of abstract automata can be defined by specifying automata homomorphisms in terms of the morphisms between five-tuples representing such abstract automata.
Example 0.2
A special case of automaton is that of a stable automaton when all its state transitions are reversible; then its state space can be seen to possess a groupoid (algebraic) structure. The category of reversible automata is then a 2-category, and also a subcategory of the 2-category of groupoids, or the groupoid category.
|
"automaton" is owned by bci1.
|
|
See Also: category of automata, general dynamic systems
| Other names: |
classical automaton, sequential machine, abstract automaton |
| Also defines: |
s-automaton, categorical automaton, sequential machine, stable automaton, state space, transition function, classical automaton, sequential machine, state space, set of automaton states, output function, automata homomorphism, \delta~, \lambda~ |
| Keywords: |
s-automaton, state space, sequential machine, stable automaton, transition function, clasical automaton, sequential machine, set of automaton states, output function, automata homomorphism |
Cross-references: groupoid category, 2-category, algebraic, groupoid, supercomputers, robots, semigroup, commute, category, category of automata, commutativity, homomorphism, composition, morphisms, commutative square diagram
There are 17 references to this object.
This is version 11 of automaton, born on 2009-01-27, modified 2009-02-26.
Object id is 442, canonical name is Automaton2.
Accessed 8542 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

