|
probability distribution functions in physics
|
(Topic)
|
|
|
This is a contributed topic on probability distribution functions and their applications in physics, mostly in spectroscopy, quantum mechanics, statistical mechanics and the theory of extended QFT operator algebras (extended symmetry, quantum groupoids with Haar measure and quantum algebroids).
Example 0.2 A classical example of a continuous probability distribution function on
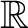 is the Gaussian distribution, or normal distribution
where 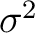 is a parameter related to the width of the distribution (measured for example at half-heigth).
In high-resolution spectroscopy, however, similar but much narrower continuous distribution functions called Lorentzians are more common; for example, high-resolution  NMR absorption spectra of neat liquids consist of such Lorentzians whereas rigid solids exhibit often only Gaussian peaks resulting from both the overlap as well as the marked broadening of Lorentzians. NMR absorption spectra of neat liquids consist of such Lorentzians whereas rigid solids exhibit often only Gaussian peaks resulting from both the overlap as well as the marked broadening of Lorentzians.
Definition 0.1 One needs to introduce first a Borel space
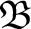 , then consider a measure space
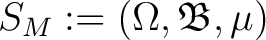 , and finally define a real function that is measurable `almost everywhere' on its domain  and is also normalized to unity. Thus, consider
 to be a measure space  . A probability distribution function (pdf) on (the domain) 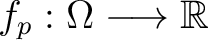 is a function
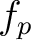 such that:
 is is 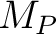 -measurable -measurable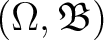 is nonnegative is nonnegative 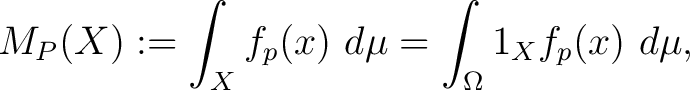 -measurable-almost everywhere. -measurable-almost everywhere.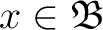 satisfies the equation satisfies the equation
Thus, a probability distribution function  induces a probability measure induces a probability measure 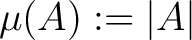 on the measure space on the measure space
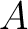 , given by , given by
for all
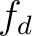 . The measure . The measure 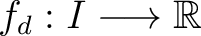 is called the associated probability measure of is called the associated probability measure of 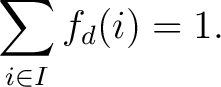 . .  and and  are different measures although both have the same underlying measurable space are different measures although both have the same underlying measurable space
 . .
A simple example of a  is any Poisson distribution is any Poisson distribution 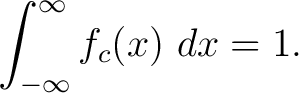 on on
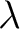 (for any real number (for any real number 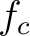 ), given by the formula ), given by the formula
for any
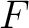 . .
Taking any probability (or measure) space 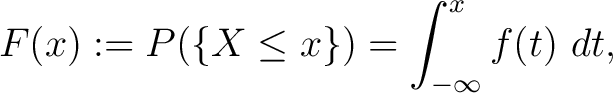 defined by the triplet defined by the triplet
 and a random variable and a random variable
 , one can construct a distribution function on , one can construct a distribution function on  by defining by defining
The resulting  function is called the distribution of function is called the distribution of  on on 
Definition 0.3 The continuous distribution (cpdf)
Consider a measure space  specified as the triplet specified as the triplet
 , that is, the set of real numbers equipped with a Lebesgue measure. Then, one can define a continuous probability distribution function (cpdf) , that is, the set of real numbers equipped with a Lebesgue measure. Then, one can define a continuous probability distribution function (cpdf)
 is simply a measurable, nonnegative almost everywhere function such that is simply a measurable, nonnegative almost everywhere function such that
The associated measure has a Radon–Nikodym derivative with respect to  equal to equal to  : :
Definition 0.4 One defines the cummulative distribution function, or cdf,  of  by the formula
for all

- 1
- B. Aniszczyk. 1991. A rigid Borel space., Proceed. AMS., 113 (4):1013-1015., available online.
- 2
- A. Connes.1979. Sur la théorie noncommutative de l' integration, Lecture Notes in Math., Springer-Verlag, Berlin, 725: 19-14.
|
Anyone with an account can edit this entry. Please help improve it!
"probability distribution functions in physics" is owned by bci1.
|
|
See Also: Fermi-Dirac distribution, quantum groupoids and C*-algebras, quantum algebroid, algebroid structures and extended symmetries
| Also defines: |
probability distribution function,  , random variable, measure space, pdf, probability measure, associated probability measure, Poisson distribution, dpdf, discrete probability distribution function, continuous probability distribution function, cpdf, distribution of , random variable, measure space, pdf, probability measure, associated probability measure, Poisson distribution, dpdf, discrete probability distribution function, continuous probability distribution function, cpdf, distribution of  on on  , cummulative distribution function, cdf, measurable function, Radon--Nikodym derivative, Gaussian distribution, normal distribution, Lorentzian, Gaussian lineshape, Lorentzian lineshape, chemical potential, quantum groupoids with Haar measure, Radon measure, Lebesgue measure , cummulative distribution function, cdf, measurable function, Radon--Nikodym derivative, Gaussian distribution, normal distribution, Lorentzian, Gaussian lineshape, Lorentzian lineshape, chemical potential, quantum groupoids with Haar measure, Radon measure, Lebesgue measure |
| Keywords: |
Fermi-Dirac distribution function |
Cross-references: formula, measurable space, domain, Borel space, solids, NMR, functions, parameter, absolute temperature, system, energy, quantum statistical mechanics, fermion, Fermi-Dirac distribution, quantum algebroids, Haar measure, operator algebras, QFT, statistical mechanics, quantum mechanics
There are 21 references to this object.
This is version 33 of probability distribution functions in physics, born on 2009-04-22, modified 2009-04-24.
Object id is 686, canonical name is ProbabilityDistributionFunctionsInPhysics.
Accessed 11234 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

