|
|
|
Main Menu
|
|
Sections
Meta
Talkback
Downloads
Information
|
|
|
|
|
|
Morita equivalence
|
(Definition)
|
|
This entry presents both the definition of Morita equivalent algebras and the Morita equivalence theorem, with a brief proof included.
Definition 1.1 Let 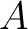 and 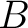 be two associative, but not necessarily commutative, algebras. Such algebras 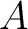 and  are called Morita equivalent, if there is an equivalence of categories between 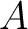 -mod and 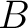 -mod.
Theorem 1.1 Morita Equivalence Theorem Commutative algebras 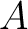 and and  are Morita equivalent if and only if they are isomorphic. are Morita equivalent if and only if they are isomorphic.
Proof. Following the above definition, isomorphic algebras are Morita equivalent. Let us assume that 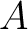 and and 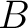 are any two such Morita equivalent associative algebras. It follows then that are any two such Morita equivalent associative algebras. It follows then that
, and thus one also has that
If 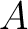 and and 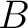 are both commutative, then by the Associative Algebra Lemma one also has that are both commutative, then by the Associative Algebra Lemma one also has that 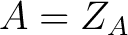 and and 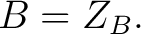
|
"Morita equivalence" is owned by bci1.
|
|
See Also: B-mod category equivalence theorem, Yoneda lemma, Morita equivalence lemma for arbitrary algebras
| Other names: |
Morita equivalent algebras |
| Also defines: |
equivalence of commutative algebras, Morita equivalent algebras |
| Keywords: |
Morita equivalence |
Cross-references: categories, theorem
There are 2 references to this object.
This is version 8 of Morita equivalence, born on 2009-06-15, modified 2009-06-15.
Object id is 806, canonical name is MoritaEquivalence.
Accessed 2341 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|
|

