|
groupoid representations induced by measure
|
(Definition)
|
|
Definition 0.1 A groupoid representation induced by measure can be defined as measure induced operators or as operators induced by a measure preserving map in the context of Haar systems with measure associated with locally compact groupoids,
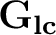 . Thus, let us consider a locally compact groupoid
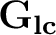 endowed with an associated Haar system
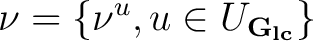 , and 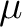 a quasi-invariant measure on
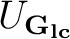 . Moreover, let
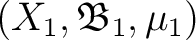 and
 be measure spaces and denote by 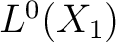 and 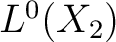 the corresponding spaces of measurable functions (with values in
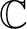 ). Let us also recall that with a measure-preserving transformation
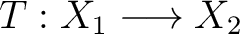 one can define an operator induced by a measure preserving map,
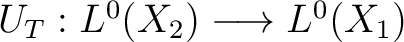 as follows.
Next, let us define
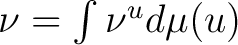 and also define and also define 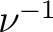 as the mapping as the mapping
 . With . With
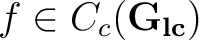 , one can now define the measure induced operator , one can now define the measure induced operator
 as an operator being defined on as an operator being defined on
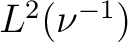 by the formula: by the formula:
Remark:
One can readily verify that :
,
and also that
 is a proper representation of is a proper representation of
 , in the sense that the latter is usually defined for groupoids. , in the sense that the latter is usually defined for groupoids.
|
"groupoid representations induced by measure" is owned by bci1.
|
|
| Also defines: |
measure-preserving transformation, groupoid representation induced by measure, operator induced by a measure preserving map |
| Keywords: |
groupoid representations, Haar systems with measure associated with locally compact groupoids |
Cross-references: groupoids, representation, formula, operator, measurable functions, measure spaces, locally compact groupoids, Haar systems, operators
There is 1 reference to this object.
This is version 6 of groupoid representations induced by measure, born on 2009-01-12, modified 2009-02-13.
Object id is 380, canonical name is GroupoidRepresentationsInducedByMeasure.
Accessed 2295 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

