|
geometrically defined double groupoid with connection
|
(Definition)
|
|
In the setting of a geometrically defined double groupoid with connection, as in [2], (resp. [3]), there is an appropriate notion of geometrically thin square. It was proven in [2], (theorem 5.2 (resp. [3], proposition 4)), that in the cases there specified geometrically and algebraically thin squares coincide.
Definition 0.1 A map
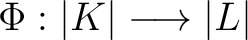 where 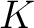 and 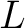 are (finite) simplicial complexes is PWL ( piecewise linear) if there exist subdivisions of  and 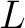 relative to which 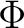 is simplicial.
We briefly recall here the related concepts involved:
Definition 0.2 A square
 in a topological space 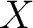 is thin if there is a factorisation of 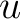 ,
where 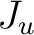 is a tree and 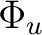 is piecewise linear (PWL, as defined next) on the boundary
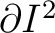 of 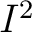 .
Definition 0.3 A tree, is defined here as the underlying space 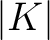 of a finite 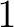 -connected 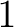 -dimensional simplicial complex 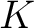 boundary
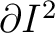 of 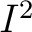 .
- 1
- Ronald Brown: Topology and Groupoids, BookSurge LLC (2006).
- 2
- Brown, R., and Hardy, J.P.L.:1976, Topological groupoids I: universal constructions, Math. Nachr., 71: 273-286.
- 3
- Brown, R., Hardie, K., Kamps, H. and T. Porter: 2002, The homotopy double groupoid of a Hausdorff space., Theory and pplications of Categories 10, 71-93.
- 4
- Ronald Brown R, P.J. Higgins, and R. Sivera.: Non-Abelian algebraic topology,(in preparation),(2008). (available here as PDF) , see also other available, relevant papers at this website.
- 5
- R. Brown and J.-L. Loday: Homotopical excision, and Hurewicz theorems, for
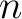 -cubes of spaces, Proc. London Math. Soc., 54:(3), 176-192,(1987). -cubes of spaces, Proc. London Math. Soc., 54:(3), 176-192,(1987).
- 6
- R. Brown and J.-L. Loday: Van Kampen Theorems for diagrams of spaces, Topology, 26: 311-337 (1987).
- 7
- R. Brown and G. H. Mosa: Double algebroids and crossed modules of algebroids, University of Wales-Bangor, Maths (Preprint), 1986.
- 8
- R. Brown and C.B. Spencer: Double groupoids and crossed modules, Cahiers Top. Géom. Diff., 17 (1976), 343-362.
|
"geometrically defined double groupoid with connection" is owned by bci1.
|
|
See Also: homotopy double groupoid of a Hausdorff space
| Also defines: |
double groupoid with connection, square, thin square, geometrically thin square, simplicial complex, simplicial, piecewise linear,  -dimensional simplicial complex, boundary -dimensional simplicial complex, boundary |
| Keywords: |
double groupoid with connection |
Cross-references: tree, topological, concepts, proposition, theorem
There are 91 references to this object.
This is version 5 of geometrically defined double groupoid with connection, born on 2009-05-01, modified 2009-05-01.
Object id is 707, canonical name is GeometricallyDefinedDoubleGroupoidWithConnection.
Accessed 5252 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

