Physics Library
 An open source physics library
Encyclopedia | Forums | Docs | Random | Template Test |  
Login
create new user
Username:
Password:
forget your password?
Main Menu
Sections

Meta

Talkback

Downloads

Information
finite quantum group (Definition)
Definition 0.1   A finite quantum group 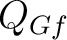$Q_{Gf}$ is a pair $(\mathbb{H},\Phi)$ of a finite-dimensional
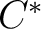$C^*$-algebra $\mathbb{H}$ with a comultiplication 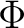$\Phi$ such that 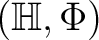$(\mathbb{H},\Phi)$ is a Hopf 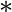$^*$-algebra.

Bibliography

1
ABE, E., Hopf Algebras, Cambridge University Press, 1977.
2
SWEEDLER, M.E., Hopf Algebras, W.A. Benjamin, inc., New York, 1969.
3
KUSTERMANS, J., VAN DAELE, A., C*-algebraic Quantum Groups arising from Algebraic Quantum Groups, Int. J. of Math. 8 (1997), 1067-1139.
4
LANCE, E.C., An explicit description of the fundamental unitary for $SU(2)_q$, Commun. Math. Phys. 164 (1994), 1-15.



"finite quantum group" is owned by bci1.
View style:
See Also: category theory

Other names:  quantum group, finite Hopf algebra
Also defines:  comultiplication in a quantum group
Keywords:  finite quantum group, comultiplication, finite Hopf algebra

There are 8 references to this object.

This is version 2 of finite quantum group, born on 2008-12-15, modified 2008-12-15.
Object id is 326, canonical name is FiniteQuantumGroup.
Accessed 1311 times total.

Classification:
Physics Classification: 03. (Quantum mechanics, field theories, and special relativity )
 03.65.Fd (Algebraic methods )
Pending Errata and Addenda
None.
Discussion
Style: Expand: Order:

No messages.

Testing some escape charachters for html category with a generator has an injective cogenerator" now escape ” with "