Physics Library
 An open source physics library
Encyclopedia | Forums | Docs | Random | Template Test |  
Login
create new user
Username:
Password:
forget your password?
Main Menu
Sections

Meta

Talkback

Downloads

Information
Borel G-space (Definition)

A (standard) Borel G-space is defined in connection with a standard Borel space which needs to be specified first.

Basic definitions

  • a. Standard Borel space.
    Definition 0.1   A standard Borel space is defined as a measurable space, that is, a set 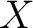$X$ equipped with a 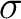$\sigma$ -algebra $\mathcal{S}$, such that there exists a Polish topology on 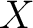$X$ with 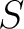$S$ its 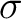$\sigma$-algebra of Borel sets.
  • b. Borel G-space.
    Definition 0.2   Let 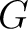$G$ be a Polish group and 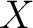$X$ a (standard) Borel space. An action 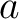$a$ of 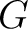$G$ on 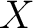$X$ is defined to be a Borel action if 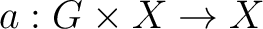$a: G \times X \to X$ is a Borel-measurable map or a Borel function. In this case, a standard Borel space 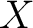$X$ that is acted upon by a Polish group with a Borel action is called a (standard) Borel G-space.
  • c. Borel morphisms.
    Definition 0.3   homomorphisms, embeddings or isomorphisms between standard Borel G-spaces are called Borel if they are Borel–measurable.
Remark 0.1   Borel G-spaces have the nice property that the product and sum of a countable sequence of Borel G-spaces $(X_n)_{n \in N}$ are also Borel G-spaces. Furthermore, the subspace of a Borel G-space determined by an invariant Borel set is also a Borel G-space.



"Borel G-space" is owned by bci1.
View style:
Also defines:  measurable space, standard Borel space, Borel set, Polish topology, sigma-algebra of Borel sets, $sigma$-algebra, Polish group, Borel morphisms, Borel function, Borel-measurable map, Borel action, invariant Borel set, Borel groupoid
Keywords:  Borel space, Borel G-space

Cross-references: G-spaces, isomorphisms, homomorphisms, Borel space
There are 10 references to this object.

This is version 5 of Borel G-space, born on 2009-04-30, modified 2009-04-30.
Object id is 701, canonical name is BorelGSpace.
Accessed 2896 times total.

Classification:
Physics Classification: 02. (Mathematical methods in physics)
Pending Errata and Addenda
None.
Discussion
Style: Expand: Order:

No messages.

Testing some escape charachters for html category with a generator has an injective cogenerator" now escape ” with "