Physics Library
 An open source physics library
Encyclopedia | Forums | Docs | Random | Template Test |  
Login
create new user
Username:
Password:
forget your password?
Main Menu
Sections

Meta

Talkback

Downloads

Information
equivalent representations of groupoids (Definition)
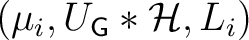
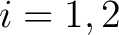
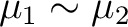
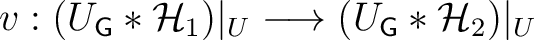
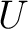
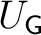
Definition 0.1   Two representations of groupoids $(\mu_i, U_{{\mathsf{G}}} * \H , L_i)$ , for $i=1,2$ are called equivalent if $\mu_1 \sim \mu_2$, and if there also exists a fiber-preserving isomorphism of analytical Hilbert space bundles $v: (U_{{\mathsf{G}}}* \H _1)\vert _U \longrightarrow (U_{{\mathsf{G}}}* \H _2)\vert _U$ , where $U$ is a measurable subset of $U_{{\mathsf{G}}}$ of null complementarity; the isomorphism $v$ 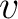also has the following property: $\hat{v}[r(x)]\hat{L}_1(x) = \hat{L}_2 \hat{v}[d(x)]$ for $x \in {\mathsf{G}}\vert _U $.



"equivalent representations of groupoids" is owned by bci1.
View style:
Also defines:  analytical Hilbert space bundles
Keywords:  analytical Hilbert space bundles, groupoid representations

Cross-references: isomorphism, groupoids, representations

This is version 2 of equivalent representations of groupoids, born on 2009-04-30, modified 2009-05-01.
Object id is 703, canonical name is EquivalentRepresentationsOfGroupoids.
Accessed 488 times total.

Classification:
Physics Classification: 02. (Mathematical methods in physics)
Pending Errata and Addenda
None.
Discussion
Style: Expand: Order:

No messages.

Testing some escape charachters for html category with a generator has an injective cogenerator" now escape ” with "