Physics Library
 An open source physics library
Encyclopedia | Forums | Docs | Random | Template Test |  
Login
create new user
Username:
Password:
forget your password?
Main Menu
Sections

Meta

Talkback

Downloads

Information
rigged Hilbert space (Definition)

In extensions of quantum mechanics [1,2], the concept of rigged Hilbert spaces allows one “to put together” the discrete spectrum of eigenvalues corresponding to the bound states (eigenvectors) with the continuous spectrum (as , for example, in the case of the ionization of an atom or the photoelectric effect).

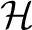Definition 0.1   A rigged Hilbert space is a pair $(\H ,\phi)$ with $\H$ a Hilbert space and 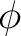$\phi$ is a dense subspace with a topological vector space structure for which the inclusion map $i$ is continuous. Between 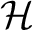$\H$ and its dual space 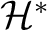$\H ^*$ there is defined the adjoint map 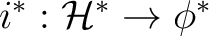$i^*: \H ^* \to \phi^*$ of the continuous inclusion map 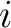$i$. The duality pairing between 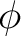$\phi$ and $\phi^*$ also needs to be compatible with the inner product on $\H$:

$\displaystyle \langle u, v\rangle_{\phi \times \phi^*} = (u, v)_{\H }$
whenever 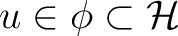$u \in \phi \subset \H$ and $v \in \H = \H ^* \subset \phi^*$.

Bibliography

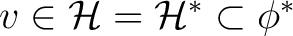1
R. de la Madrid, “The role of the rigged Hilbert space in Quantum Mechanics.”, Eur. J. Phys. 26, 287 (2005); $quant-ph/0502053$.
2
J-P. Antoine, “Quantum Mechanics Beyond Hilbert Space” (1996), appearing in Irreversibility and Causality, Semigroups and Rigged Hilbert Spaces, Arno Bohm, Heinz-Dietrich Doebner, Piotr Kielanowski, eds., Springer-Verlag, $ISBN 3-540-64305-2$.



"rigged Hilbert space" is owned by bci1.
View style:
Other names:  Gelfand triple, nuclear Frechet space
Also defines:  adjoint map, i*
Keywords:  rigged Hilbert space

Cross-references: inner product, duality, dual space, vector space, topological, Hilbert space, photoelectric effect, spectrum, concept, quantum mechanics
There are 13 references to this object.

This is version 9 of rigged Hilbert space, born on 2009-03-02, modified 2009-03-03.
Object id is 558, canonical name is RiggedHilbertSpace.
Accessed 1811 times total.

Classification:
Physics Classification: 00. (GENERAL)
 02. (Mathematical methods in physics)
 03. (Quantum mechanics, field theories, and special relativity )
 03.65.Fd (Algebraic methods )
Pending Errata and Addenda
None.
Discussion
Style: Expand: Order:

No messages.

Testing some escape charachters for html category with a generator has an injective cogenerator" now escape ” with "