|
|
|
Main Menu
|
|
Sections
Meta
Talkback
Downloads
Information
|
|
|
|
|
|
proper generator in a Grothendieck category
|
(Topic)
|
|
Definition 0.1 Let
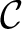 be a category. A family of its objects
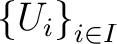 is said to be a family of generators of
 if for every pair of distinct morphisms
 there is a morphism
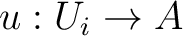 for some index 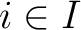 such that
 .
One notes that in an additive category,
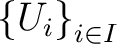 is a family of generators if and only if for each nonzero morphism is a family of generators if and only if for each nonzero morphism 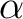 in in
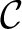 there is a morphism there is a morphism
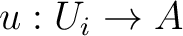 such that such that
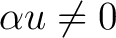 . .
Definition 0.2 An object  in
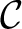 is called a generator for
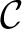 if
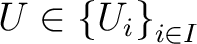 with
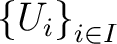 being a family of generators for
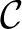 .
Equivalently, (viz. Mitchell) 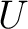 is a generator for is a generator for
 if and only if the set-valued functor if and only if the set-valued functor 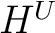 is an imbedding functor. is an imbedding functor.
Theorem 0.1 Any commutative ring is the endomorphism ring of a proper generator in a suitably chosen Grothendieck category.
|
"proper generator in a Grothendieck category" is owned by bci1.
|
|
Cross-references: commutative ring, isomorphism, monomorphism, Grothendieck category, functor, additive category, morphisms, generators, objects, category
This is version 3 of proper generator in a Grothendieck category, born on 2009-02-02, modified 2009-02-02.
Object id is 470, canonical name is ProperGeneratorInAGrothendieckCategory.
Accessed 960 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|
|

