A sundial located in New York City (longitude
 W) shows a local apparent solar time of 12:00 PM when the sun is at its highest point in the sky. However, the standard time in New York (Eastern Time Zone, UTC-5) is different due to the equation of time and longitude correction. W) shows a local apparent solar time of 12:00 PM when the sun is at its highest point in the sky. However, the standard time in New York (Eastern Time Zone, UTC-5) is different due to the equation of time and longitude correction.
- Calculate the mean solar time corresponding to this observation.
- Determine the difference between local apparent solar time and mean solar time if the equation of time on that day is
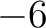 minutes. minutes.
- What is the standard clock time (Eastern Time) for this event, considering the longitude-based time zone adjustment?
- Longitude of New York City:
 W. W.
- Reference longitude for Eastern Time Zone:
 W. W.
- Equation of Time on the given day:
 minutes. minutes.
1. Mean Solar Time (MST) is related to Local Apparent Solar Time (LAST) by the equation:
MST  LAST 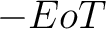 2. Longitude Correction: The time zone is based on
 W, but New York City is at W, but New York City is at
 W. The difference is: W. The difference is:
Since
 hour, the time difference is: hour, the time difference is:
3. Standard Clock Time: The mean solar time must be adjusted by  to get the standard time: to get the standard time:
The mean solar time is
 PM, and the standard clock time is approximately PM, and the standard clock time is approximately
 PM. PM.
This is an example problem generated from DeepSeek AI using prompt, "For a physics class can you give an example problem for mean solar time and write it in latex".
|

