|
The assumption of linear least squares is that there is a linear relationship between our measurements 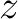 and the variables to be estimated and the variables to be estimated 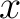
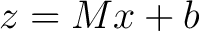 |
(1) |
For this example let us assume that our measurements are given in Table 1 and you can see them plotted in Figure 1.
| x |
-3.0 |
-2.5 |
-2.0 |
-1.5 |
-1.0 |
-0.5 |
0.0 |
0.5 |
1.0 |
1.5 |
| z |
-1.0 |
-0.25 |
0.0 |
0.25 |
0.4 |
0.7 |
1.0 |
1.1 |
1.4 |
1.8 |
Table 1: Example Data
The linear least squares solution to fit the given data is given by the equation
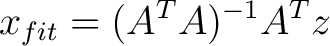 |
(2) |
The only not so obvious step before using a tool like Matlab, is to form the 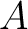 matrix, which is a combination of an identity vector and matrix, which is a combination of an identity vector and 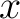 as column vectors, such that as column vectors, such that
This is clarified by looking at the example code in Matlab, LinearLeastSquares.m. A plot of fitting the measurement data with a line such that it minimizes the the mean square of the error is shown in Figure 1.
The equation of the line to fit this data is then
Figure 1: Linear Fit of Example Data (Matlab)
Figure 1: Linear Fit of Example Data (rlplot)
| 
