|
|
|
Main Menu
|
|
Sections
Meta
Talkback
Downloads
Information
|
|
|
|
|
|
Enriched Category Theory
|
(Topic)
|
|
|
This is a new, contributed topic on enrichments of category theory, including a weak Yoneda lemma, functor categories, 2-categories and representable V-functors.
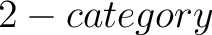 VCAT for a monoidal V category
 , such as
Tensor products and duality Closed and bi-closed bimonoidal categories
Representable V functors Extraordinary V naturality and the V naturality of the canonical maps
The isomorphism
![$[A \times [B, C]] \cong [A,[B,C]]$](http://images.physicslibrary.org/cache/objects/888/l2h/img8.png "$[A \times [B, C]] \cong [A,[B,C]]$")
Indexing types; limits and colimits; Yoneda isomorphisms
Preservation of limits and colimits
The connection with classical conical limits when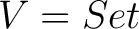 
The definition of Kan extensions: their expressibility by limits and colimits
more to come
|
Anyone with an account can edit this entry. Please help improve it!
"Enriched Category Theory" is owned by bci1.
|
|
| Keywords: |
Kan adjointness, enriched categories, weak Yoneda Lemma |
Cross-references: types, isomorphism, functors, duality, tensor, category, 2-categories, functor categories, Yoneda lemma, category theory
This is version 15 of Enriched Category Theory, born on 2010-11-01, modified 2010-11-07.
Object id is 888, canonical name is EnrichedCategoryTheory.
Accessed 451 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|
|
![$[A,B]$](http://images.physicslibrary.org/cache/objects/888/l2h/img5.png "$[A,B]$")
![$[A,B]$](http://images.physicslibrary.org/cache/objects/888/l2h/img7.png "$[A,B]$")
