|
Let
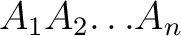 be an be an  -gon which is supposed to have a constant surface-density in all of its points, -gon which is supposed to have a constant surface-density in all of its points, 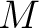 the centre of mass of the polygon and the centre of mass of the polygon and  the origin. Then the position vector of the origin. Then the position vector of  with respect to with respect to  is
is
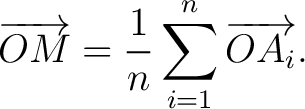 |
(1) |
We can of course take especially  , and thus , and thus
In the special case of the triangle 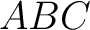 we have we have
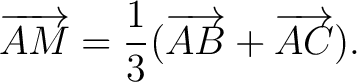 |
(2) |
The centre of mass of a triangle is the common point of its medians.
Remark. An analogical result with (2) concerns also the homogeneous tetrahedron 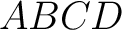 , ,
and any 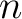 -dimensional simplex (cf. the midpoint of line segment: -dimensional simplex (cf. the midpoint of line segment:
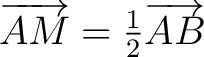 ). ).
| 
