Physics Library
 An open source physics library
Encyclopedia | Forums | Docs | Random | Template Test |  
Login
create new user
Username:
Password:
forget your password?
Main Menu
Sections

Meta

Talkback

Downloads

Information
category of quantum automata (Definition)
Definition 0.1   Let us recall that as a Quantum Algebraic Topology object, a quantum automaton is defined by the quantum triple $Q_A =(\mathcal G,\H -\Re_G, Aut(\mathcal G)$), where $\mathcal G$ is a (locally compact) quantum groupoid, $\H -\Re_G$ are the unitary representations of $\mathcal G$ on rigged Hilbert spaces $\Re_G$ of quantum states and quantum operators on the Hilbert space $\H$, and $Aut(\mathcal G)$ is the transformation, or automorphism groupoid of quantum transitions that represents all flip-flop quantum transitions of one cubit each between the permitted quantum states of the quantum automaton.

With the data from above definition we can now define also the category of quantum automata as follows.

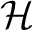Definition 0.2   The category of quantum automata $\mathcal{\mathcal Q}_A$ is defined as an algebraic category whose objects are triples $(\H , \Delta: \H\rightarrow \H , \mu)$ (where $\H$ is either a Hilbert space or a rigged Hilbert space of quantum states and operators acting on 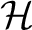$\H$, and 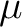$\mu$ is a measure related to the quantum logic, 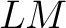$LM$, and (quantum) transition probabilities of this quantum system), and whose morphisms are defined between such triples by homomorphisms of Hilbert spaces, 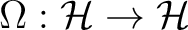$\O : \H\rightarrow \H$, naturally compatible with the operators 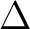$\Delta$, and by homomorphisms between the associated Haar measure systems.

An alternative definition is also possible based on Quantum Algebraic Topology.

Definition 0.3   A quantum algebraic topology definition of the category of quantum algebraic automata involves the objects specified above in Definition 0.1 as quantum automaton triples 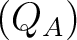$(Q_A)$, and quantum automata homomorphisms defined between such triples; these 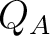$Q_A$ morphisms are defined by groupoid homomorphisms 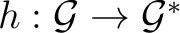$h: \mathcal G\rightarrow \mathcal G^*$ and 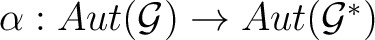$\alpha: Aut(\mathcal G) \rightarrow Aut(\mathcal G^*)$, together with unitarity preserving mappings 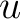$u$ between unitary representations of 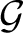$\mathcal G$ on rigged Hilbert spaces (or Hilbert space bundles).



"category of quantum automata" is owned by bci1.
View style:
See Also: category of automata


Cross-references: Hilbert space bundles, groupoid homomorphisms, quantum automata, algebraic, category, Haar measure, homomorphisms, morphisms, system, quantum logic, operators, algebraic category, groupoid, Hilbert space, quantum operators, rigged Hilbert spaces, representations, quantum groupoid, quantum automaton, object, Quantum Algebraic Topology
There are 7 references to this object.

This is version 1 of category of quantum automata, born on 2009-02-14.
Object id is 522, canonical name is CategoryOfQuantumAutomata.
Accessed 542 times total.

Classification:
Physics Classification: 00. (GENERAL)
 02. (Mathematical methods in physics)
 03. (Quantum mechanics, field theories, and special relativity )
 03.65.Fd (Algebraic methods )
Pending Errata and Addenda
None.
Discussion
Style: Expand: Order:

No messages.

Testing some escape charachters for html category with a generator has an injective cogenerator" now escape ” with "