Physics Library
 An open source physics library
Encyclopedia | Forums | Docs | Random | Template Test |  
Login
create new user
Username:
Password:
forget your password?
Main Menu
Sections

Meta

Talkback

Downloads

Information
Borel morphism (Definition)
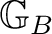Definition 0.1   Let ${\mathbb{G}}_B$ and ${\mathbb{G}}_B$* be two groupoids whose object spaces are Borel. An algebraic morphism from 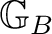${\mathbb{G}}_B$ to 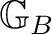${\mathbb{G}}_B$* is defined as a left action of 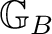${\mathbb{G}}_B$ on 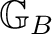${\mathbb{G}}_B$* which commutes with the multiplication on 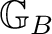${\mathbb{G}}_B$. Such an algebraic morphism between Borel groupoids is said to be a Borel morphism if the action of 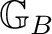${\mathbb{G}}_B$ on 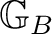${\mathbb{G}}_B$* is Borel (viz. ref. [1])

Bibliography

1
M.R. Buneci. 2006., Groupoid C*-Algebras., Surveys in Mathematics and its Applications, Volume 1: 71–98.



"Borel morphism" is owned by bci1.
View style:

Cross-references: Borel groupoids, commutes, morphism, algebraic, object, groupoids

This is version 1 of Borel morphism, born on 2009-02-04.
Object id is 488, canonical name is BorelMorphism.
Accessed 394 times total.

Classification:
Physics Classification: 00. (GENERAL)
Pending Errata and Addenda
None.
Discussion
Style: Expand: Order:

No messages.

Testing some escape charachters for html category with a generator has an injective cogenerator" now escape ” with "