|
2-category of double groupoids
|
(Topic)
|
|
|
This is a topic entry on the 2-category of double groupoids.
Definition 1.1 Let us recall that if 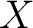 is a topological space, then a double goupoid
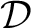 is defined by the following categorical diagram of linked groupoids and sets:
![$\displaystyle \mathcal D:= \vcenter{\xymatrix @=3pc {S \ar @<1ex> [r] ^{s^1} \a... ... [d]_s \ V \ar [u] \ar @<1ex> [r] ^s \ar @<-1ex> [r] _t & M \ar [l] \ar[u]}},$ $\displaystyle \mathcal D:= \vcenter{\xymatrix @=3pc {S \ar @<1ex> [r] ^{s^1} \a... ... [d]_s \ V \ar [u] \ar @<1ex> [r] ^s \ar @<-1ex> [r] _t & M \ar [l] \ar[u]}},$](http://images.physicslibrary.org/cache/objects/454/l2h/img3.png) |
(1.1) |
where 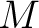 is a set of points, is a set of points, 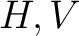 are two groupoids (called, respectively, “horizontal” and “vertical” groupoids) , and are two groupoids (called, respectively, “horizontal” and “vertical” groupoids) , and 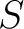 is a set of squares with two composition laws, is a set of squares with two composition laws,  and and  (as first defined and represented in ref. [1] by Brown et al.) . A simplified notion of a thin square is that of “a continuous map from the unit square of the real plane into (as first defined and represented in ref. [1] by Brown et al.) . A simplified notion of a thin square is that of “a continuous map from the unit square of the real plane into 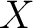 which factors through a tree” ([1]). which factors through a tree” ([1]).
The algebraic composition laws,  and and  , employed above to define a double groupoid , employed above to define a double groupoid
 allow one also to define allow one also to define
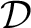 as a groupoid internal to the category of groupoids. Thus, in the particular case of a Hausdorff space, as a groupoid internal to the category of groupoids. Thus, in the particular case of a Hausdorff space, 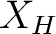 , a double groupoid called the homotopy double groupoid of , a double groupoid called the homotopy double groupoid of  can be denoted as follows can be denoted as follows
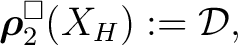 where  is in this case a thin square. Thus, the construction of a homotopy double groupoid is based upon the geometric notion of thin square that extends the notion of thin relative homotopy as discussed in ref. [1]. One notes however a significant distinction between a homotopy 2-groupoid and homotopy double groupoid construction; thus, the construction of the is in this case a thin square. Thus, the construction of a homotopy double groupoid is based upon the geometric notion of thin square that extends the notion of thin relative homotopy as discussed in ref. [1]. One notes however a significant distinction between a homotopy 2-groupoid and homotopy double groupoid construction; thus, the construction of the 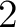 -cells of the homotopy double groupoid is based upon a suitable cubical approach to the notion of thin -cells of the homotopy double groupoid is based upon a suitable cubical approach to the notion of thin  -cube, whereas the construction of the 2-cells of the homotopy -cube, whereas the construction of the 2-cells of the homotopy 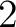 -groupoid can be interpreted by means of a globular notion of thin -groupoid can be interpreted by means of a globular notion of thin 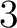 -cube. “The homotopy double groupoid of a space, and the related homotopy -cube. “The homotopy double groupoid of a space, and the related homotopy 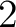 -groupoid, are constructed directly from the cubical singular complex and so (they) remain close to geometric intuition in an almost classical way” (viz. [1]). -groupoid, are constructed directly from the cubical singular complex and so (they) remain close to geometric intuition in an almost classical way” (viz. [1]).
Definition 1.2 The 2-category,
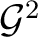 – whose objects (or 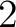 -cells) are the above diagrams
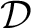 that define double groupoids, and whose 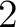 -morphisms are functors
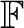 between double groupoid
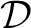 diagrams– is called the double groupoid 2-category, or the 2-category of double groupoids.
Remark 1.1
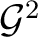 is a relatively simple example of a category of diagrams, or a 1-supercategory, 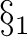 .
- 1
- R. Brown, K.A. Hardie, K.H. Kamps and T. Porter., A homotopy double groupoid of a Hausdorff space , Theory and Applications of Categories 10,(2002): 71-93.
- 2
- R. Brown and C.B. Spencer: Double groupoids and crossed modules, Cahiers Top. Géom.Diff., 17 (1976), 343–362.
- 3
- R. Brown and G. H. Mosa: Double algebroids and crossed modules of algebroids, University of Wales–Bangor, Maths Preprint, 1986.
- 4
- K.A. Hardie, K.H. Kamps and R.W. Kieboom., A homotopy 2-groupoid of a Hausdorff Applied Categorical Structures, 8 (2000): 209-234.
- 5
- Al-Agl, F.A., Brown, R. and R. Steiner: 2002, Multiple categories: the equivalence of a globular and cubical approach, Adv. in Math, 170: 711-118.
|
"2-category of double groupoids" is owned by bci1.
|
|
See Also: 2-category, groupoid, higher dimensional algebra
| Keywords: |
2-category, double groupoids, 2-category of double groupoids. |
Cross-references: category, 2-category, functors, diagrams, objects, 2-groupoid, homotopy, double groupoid, composition laws, algebraic, thin square, groupoids, categorical diagram, topological
There is 1 reference to this object.
This is version 9 of 2-category of double groupoids, born on 2009-01-31, modified 2009-04-18.
Object id is 454, canonical name is 2CategoryOfDoubleGroupoids.
Accessed 1744 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

