|
The angle of rotation can be found from the trace of the direction cosine matrix to axis angle of rotation matrix
Noting that the axis of rotation is a unit vector and has a length of 1 means
therefore
rearranging gives
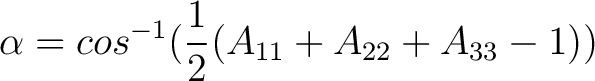 |
(1) |
Inverse cosine is a multivalued function and there are 2 possible solutions for 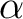 . Normally, the convention is to choose the principle value such that . Normally, the convention is to choose the principle value such that
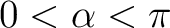
As long as 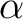 is not zero, the unit vector is given by is not zero, the unit vector is given by
![$\displaystyle \left[ \begin{array}{c} e_1 \ e_2 \ e_3 \end{array} \right] =... ...2 sin(\alpha)} \ \dfrac{(A_{12} - A_{21})}{2 sin(\alpha)} \end{array} \right]$ $\displaystyle \left[ \begin{array}{c} e_1 \ e_2 \ e_3 \end{array} \right] =... ...2 sin(\alpha)} \ \dfrac{(A_{12} - A_{21})}{2 sin(\alpha)} \end{array} \right]$](http://images.physicslibrary.org/cache/objects/89/l2h/img8.png) |
(2) |
Above equation should be proved at some time...
| 
