Physics Library
 An open source physics library
Encyclopedia | Forums | Docs | Random | Template Test |  
Login
create new user
Username:
Password:
forget your password?
Main Menu
Sections

Meta

Talkback

Downloads

Information
regular measure (Definition)
Definition 0.1   A regular measure 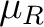$\mu_R$ on a topological space 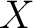$X$ is a measure on 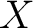$X$ such that for each 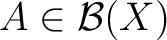$A \in \mathcal{B}(X) $ , with 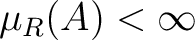$\mu_R (A) < \infty$), and each 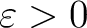$\varepsilon > 0$ there exist a compact subset 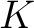$K$ of 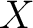$X$ and an open subset 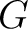$G$ of 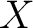$X$ with 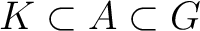$K \subset A \subset G$, such that for all sets 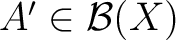$A' \in \mathcal{B}(X)$ with 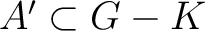$A' \subset G - K$, one has $\mu_R(A') <\varepsilon$.



"regular measure" is owned by bci1.
View style:
Keywords:  regular measure

Cross-references: topological

This is version 1 of regular measure, born on 2009-05-09.
Object id is 737, canonical name is RegularMeasure.
Accessed 734 times total.

Classification:
Physics Classification: 00. (GENERAL)
 02. (Mathematical methods in physics)
Pending Errata and Addenda
None.
Discussion
Style: Expand: Order:

No messages.

Testing some escape charachters for html category with a generator has an injective cogenerator" now escape ” with "