|
|
|
Main Menu
|
|
Sections
Meta
Talkback
Downloads
Information
|
|
|
|
|
|
using convolution to find Laplace transforms
|
(Definition)
|
|
|
We start from the relations (see the table of Laplace transforms)
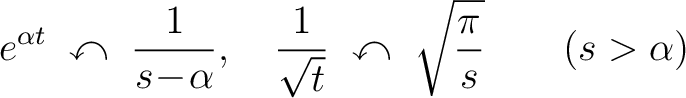 |
(1) |
where the curved arrows point from the Laplace-transformed functions to the original functions. Setting
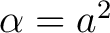 and dividing by and dividing by
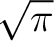 in (1), the convolution property of Laplace transform yields
The substitution in (1), the convolution property of Laplace transform yields
The substitution
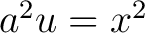 then gives
Thus we may write the formula then gives
Thus we may write the formula
 |
(2) |
Moreover, we obtain
whence we have the other formula
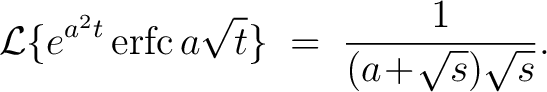 |
(3) |
One can utilise the formula (3) for evaluating the improper integral
We have
(see the table of Laplace transforms). Dividing this by
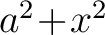 and integrating from 0 to and integrating from 0 to  , we can continue as follows:
Consequently,
and especially , we can continue as follows:
Consequently,
and especially
|
Anyone with an account can edit this entry. Please help improve it!
"using convolution to find Laplace transforms" is owned by pahio.
|
|
See Also: table of Laplace transforms
Cross-references: formula, Laplace transform, functions, table of Laplace transforms
This is version 3 of using convolution to find Laplace transforms, born on 2009-05-04, modified 2009-05-05.
Object id is 733, canonical name is UsingConvolutionToFindLaplaceTransforms.
Accessed 1009 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|
|

