|
Let's consider the d'Alembert's solution
![$\displaystyle u(x,\,t) \,:=\, \frac{1}{2}[f(x\!-\!ct)+f(x\!+\!ct)]+\frac{1}{2c}\int_{x-ct}^{x+ct}g(s)\,ds$ $\displaystyle u(x,\,t) \,:=\, \frac{1}{2}[f(x\!-\!ct)+f(x\!+\!ct)]+\frac{1}{2c}\int_{x-ct}^{x+ct}g(s)\,ds$](http://images.physicslibrary.org/cache/objects/661/l2h/img1.png) |
(1) |
of the wave equation in one dimension in the special case when the other initial condition is
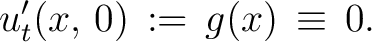 |
(2) |
We shall see that the solution is equivalent with the solution of D. Bernoulli.
We expand the given function 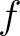 to the Fourier sine series on the interval to the Fourier sine series on the interval ![$[0,\,p]$ $[0,\,p]$](http://images.physicslibrary.org/cache/objects/661/l2h/img4.png) : :
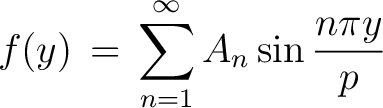 with 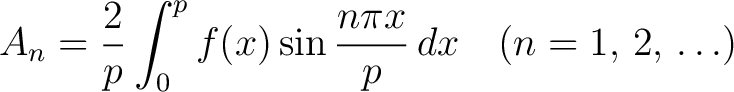
![$\displaystyle u(x,\,t) = \frac{1}{2}[f(x\!-\!ct)+f(x\!+\!ct)] = \sum_{n=1}^\infty A_n\cos\frac{n\pi ct}{p}\sin\frac{n\pi x}{p},$ $\displaystyle u(x,\,t) = \frac{1}{2}[f(x\!-\!ct)+f(x\!+\!ct)] = \sum_{n=1}^\infty A_n\cos\frac{n\pi ct}{p}\sin\frac{n\pi x}{p},$](http://images.physicslibrary.org/cache/objects/661/l2h/img8.png) |
(3) |
which indeed is the solution of D. Bernoulli in the case
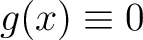 . .
Note. The solution (3) of the wave equation is especially simple in the special case where one has besides (2) the sine-formed initial condition
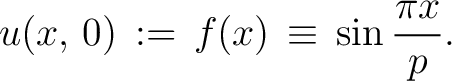 |
(4) |
Then 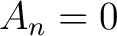 for every for every 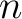 except 1, and one obtains except 1, and one obtains
 |
(5) |
Remark. In the case of quantum systems one has Schrödinger's wave equation whose solutions are different from the above.
| 
