![[parent]](https://images.physicslibrary.org/images/uparrow.png) CCR representation theory
CCR representation theory
|
(Topic)
|
|
Definition 0.1 In connection with the Schrödinger representation, one defines a Schrödinger d-system as a set
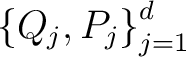 of self-adjoint operators on a Hilbert space
 (such as the position and momentum operators, for example) when there exist mutually orthogonal closed subspaces
 of
 such that
 with the following two properties:
- (i) each
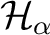 reduces all reduces all 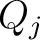 and all and all 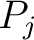 ; ;
- (ii) the set
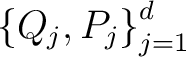 is, in each is, in each
 , unitarily equivalent to the Schrödinger representation , unitarily equivalent to the Schrödinger representation
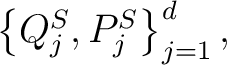 [8]. [8].
Definition 0.2 A set
 of self-adjoint operators on a Hilbert space
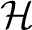 is called a Weyl representation with 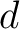 degrees of freedom degrees of freedom if  and 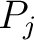 satisfy the Weyl relations:
-
-
-
with
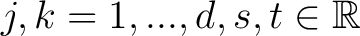 . .
The Schrödinger representation
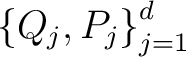 is a Weyl representation of CCR. is a Weyl representation of CCR.
Von Neumann established a uniqueness theorem: if the Hilbert space
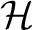 is separable, then every Weyl representation of CCR with is separable, then every Weyl representation of CCR with  degrees of freedom is a Schrödinger degrees of freedom is a Schrödinger 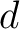 -system ([6]). Since the pioneering work of von Neumann [6] there have been numerous reports published concerning representation theory of CCR (viz. ref. [8] and references cited therein). -system ([6]). Since the pioneering work of von Neumann [6] there have been numerous reports published concerning representation theory of CCR (viz. ref. [8] and references cited therein).
- 1
- Arai A., Characterization of anticommutativity of self-adjoint operators in connection with Clifford algebra and applications, Integr. Equat. Oper. Th., 1993, v.17, 451–463.
- 2
- Arai A., Commutation properties of anticommuting self-adjoint operators, spin representation and Dirac operators, Integr. Equat. Oper. Th., 1993, v.16, 38–63.
- 3
- Arai A., Analysis on anticommuting self–adjoint operators, Adv. Stud. Pure Math., 1994, v.23, 1–15.
- 4
- Arai A., Scaling limit of anticommuting self-adjoint operators and applications to Dirac operators, Integr. Equat. Oper. Th., 1995, v.21, 139–173.
- 5
- Arai A., Some remarks on scattering theory in supersymmetric quantum mechanics, J. Math. Phys., 1987, V.28, 472–476.
- 6
- von Neumann J., Die Eindeutigkeit der Schrödingerschen Operatoren, Math. Ann., 1931, v.104, 570–578.
- 7
- Pedersen S., Anticommuting self–adjoint operators, J. Funct. Anal., 1990, V.89, 428–443.
- 8
- Putnam C. R., Commutation Properties of Hilbert Space Operators, Springer, Berlin, 1967.
- 9
- Reed M. and Simon B., Methods of Modern Mathematical Physics., vol.I, Academic Press, New York, 1972.
|
"CCR representation theory" is owned by bci1.
|
|
| Other names: |
representation theory of canonical commutation relations |
| Also defines: |
Schroedinger d-system |
| Keywords: |
representation theory of canonical commutation relations, CCR |
This object's parent.
Cross-references: work, theorem, CCR, relations, momentum, position, Hilbert space, operators, representation
This is version 11 of CCR representation theory, born on 2009-02-21, modified 2009-02-21.
Object id is 548, canonical name is CCRRepresentationTheory.
Accessed 2281 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

