|
Borel groupoid
|
(Definition)
|
|
- Borel function
- Borel groupoid
Definition 0.2 Let
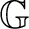 be a groupoid and
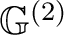 a subset of
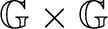 – the set of its composable pairs. A Borel groupoid is defined as a groupoid
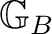 such that
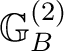 is a Borel set in the product structure on
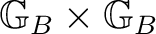 , and also such that the functions
 from
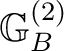 to
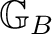 , and
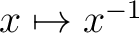 from
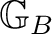 to
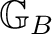 are all (measurable) Borel functions (ref. [ 1]).
 becomes an analytic groupoid if its Borel structure is analytic. becomes an analytic groupoid if its Borel structure is analytic.
A Borel space
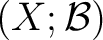 is called analytic if it is countably separated, and also if it is the image of a Borel function from a standard Borel space. is called analytic if it is countably separated, and also if it is the image of a Borel function from a standard Borel space.
- 1
- M.R. Buneci. 2006., Groupoid C*-Algebras., Surveys in Mathematics and its Applications, Volume 1, p.75 .
|
"Borel groupoid" is owned by bci1.
|
|
Cross-references: standard Borel space, Borel space, groupoid, Borel set, function, Borel function
There are 4 references to this object.
This is version 2 of Borel groupoid, born on 2009-02-04, modified 2010-04-28.
Object id is 486, canonical name is BorelGroupoid.
Accessed 1340 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

