|
nuclear C*-algebra
|
(Definition)
|
|
Definition 0.1 A C*-algebra 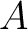 is called a nuclear C*-algebra if all C*-norms on every algebraic tensor product
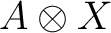 , of 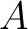 with any other C*-algebra 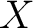 , agree with, and also equal the spatial C*-norm ( viz Lance, 1981). Therefore, there is a unique completion of
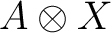 to a C*-algebra , for any other C*-algebra  .
- All commutative C*-algebras and all finite-dimensional C*-algebras
- group C*-algebras of amenable groups
- Crossed products of strongly amenable C*-algebras by amenable discrete groups,
- type
 C*-algebras. C*-algebras.
In general terms, a 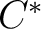 -algebra is exact if it is isomorphic with a -algebra is exact if it is isomorphic with a  -subalgebra of some nuclear -subalgebra of some nuclear 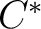 -algebra. The precise definition of an exact -algebra. The precise definition of an exact 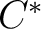 -algebra follows. -algebra follows.
Definition 0.2 Let 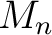 be a matrix space, let
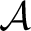 be a general operator space, and also let
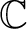 be a C*-algebra. A 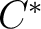 -algebra
 is exact if it is `finitely representable' in 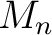 , that is, if for every finite dimensional subspace 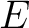 in
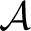 and quantity
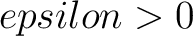 , there exists a subspace 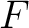 of some 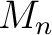 , and also a linear isomorphism 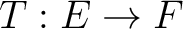 such that the 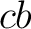 -norm
The group C*-algebras for the free groups on two or more generators are not nuclear. Furthermore, a 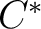 -subalgebra of a nuclear C*-algebra need not be nuclear. -subalgebra of a nuclear C*-algebra need not be nuclear.
- 1
- E. C. Lance. 1981. Tensor Products and nuclear C*-algebras., in Operator Algebras and Applications, R.V. Kadison, ed., Proceed. Symp. Pure Maths., 38: 379-399, part 1.
- 2
- N. P. Landsman. 1998. “Lecture notes on
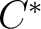 -algebras, Hilbert -algebras, Hilbert 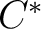 -Modules and Quantum Mechanics”, pp. 89 a graduate level preprint discussing general C*-algebras in Postscript format. -Modules and Quantum Mechanics”, pp. 89 a graduate level preprint discussing general C*-algebras in Postscript format.
|
"nuclear C*-algebra" is owned by bci1.
|
|
| Keywords: |
nuclear C*-algebras |
Cross-references: generators, isomorphism, operator, matrix, type, group, tensor, algebraic, C*-algebra
This is version 1 of nuclear C*-algebra, born on 2009-02-02.
Object id is 465, canonical name is NuclearCAlgebra.
Accessed 980 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

