|
Let
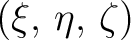 be a point bearing a mass be a point bearing a mass 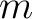 and and
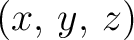 a variable point. If the distance of these points is a variable point. If the distance of these points is  , we can define the potential of , we can define the potential of
 in in
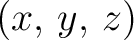 as as
The relevance of this concept appears from the fact that its partial derivatives
are the components of the gravitational force with which the material point
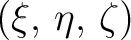 acts on one mass unit in the point acts on one mass unit in the point
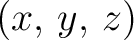 (provided that the measure units are chosen suitably). (provided that the measure units are chosen suitably).
The potential of a set of points
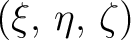 is the sum of the potentials of individual points, i.e. it may lead to an integral. is the sum of the potentials of individual points, i.e. it may lead to an integral.
We determine the potential of all points
 of a hollow ball, where the matter is located between two concentric spheres with radii of a hollow ball, where the matter is located between two concentric spheres with radii  and and
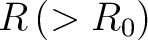 . Here the density of mass is assumed to be presented by a continuous function . Here the density of mass is assumed to be presented by a continuous function
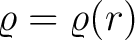 at the distance at the distance  from the centre from the centre  . Let . Let  be the distance from be the distance from  of the point of the point 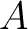 , where the potential is to be determined. We chose , where the potential is to be determined. We chose  the origin and the ray the origin and the ray 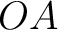 the positive the positive 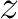 -axis. -axis.
For obtaining the potential in 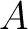 we must integrate over the ball shell where we must integrate over the ball shell where
 . We use the spherical coordinates . We use the spherical coordinates 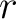 , , 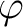 and and 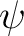 which are tied to the Cartesian coordinates via which are tied to the Cartesian coordinates via
for attaining all points we set
The cosines law implies that
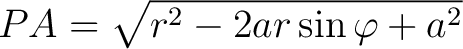 . Thus the potential is the triple integral . Thus the potential is the triple integral
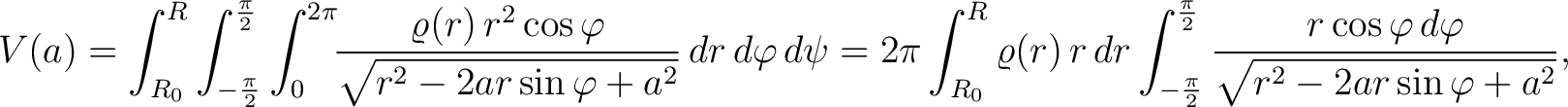 |
(1) |
where the factor
 is the coefficient for the coordinate changing is the coefficient for the coordinate changing
We get from the latter integral
![$\displaystyle \int_{-\frac{\pi}{2}}^\frac{\pi}{2} \frac{r\cos\varphi\,d\varphi}... ...frac{\pi}{2}}\sqrt{r^2-2ar\sin\varphi+a^2} = \frac{1}{a}[(r+a)-\vert r-a\vert].$ $\displaystyle \int_{-\frac{\pi}{2}}^\frac{\pi}{2} \frac{r\cos\varphi\,d\varphi}... ...frac{\pi}{2}}\sqrt{r^2-2ar\sin\varphi+a^2} = \frac{1}{a}[(r+a)-\vert r-a\vert].$](http://images.physicslibrary.org/cache/objects/250/l2h/img35.png) |
(2) |
Accordingly we have the two cases:
 . The point . The point 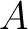 is outwards the hollow ball, i.e. is outwards the hollow ball, i.e. 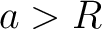 . Then we have . Then we have
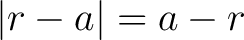 for all for all
![$r\in[R_0,\,R]$ $r\in[R_0,\,R]$](http://images.physicslibrary.org/cache/objects/250/l2h/img40.png) . The value of the integral (2) is . The value of the integral (2) is
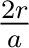 , and (1) gets the form , and (1) gets the form
where 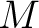 is the mass of the hollow ball. Thus the potential outwards the hollow ball is exactly the same as in the case that all mass were concentrated to the centre. A correspondent statement concerns the attractive force is the mass of the hollow ball. Thus the potential outwards the hollow ball is exactly the same as in the case that all mass were concentrated to the centre. A correspondent statement concerns the attractive force
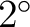 . The point . The point 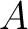 is in the cavity of the hollow ball, i.e. is in the cavity of the hollow ball, i.e. 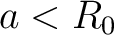 . Then . Then
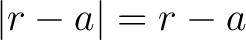 on the interval of integration of (2). The value of (2) is equal to 2, and (1) yields on the interval of integration of (2). The value of (2) is equal to 2, and (1) yields
which is independent on 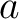 . That is, the potential of the hollow ball, when the density of mass depends only on the distance from the centre, has in the cavity a constant value, and the hollow ball influences in no way on a mass inside it. . That is, the potential of the hollow ball, when the density of mass depends only on the distance from the centre, has in the cavity a constant value, and the hollow ball influences in no way on a mass inside it.
- 1
- ERNST LINDELÖF: Differentiali- ja integralilasku ja sen sovellutukset II. Mercatorin Kirjapaino Osakeyhtiö, Helsinki (1932).
| 
