|
CW-complex representation theorems in QAT
|
(Theorem)
|
|
QAT theorems for quantum state spaces of spin networks and quantum spin foams based on 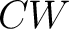 , , 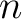 -connected models and fundamental theorems. -connected models and fundamental theorems.
Let us consider first a lemma in order to facilitate the proof of the following theorem concerning spin networks and quantum spin foams.
Lemma Let 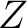 be a be a 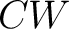 complex that has the (three–dimensional) Quantum Spin `Foam' (QSF) as a subspace. Furthermore, let complex that has the (three–dimensional) Quantum Spin `Foam' (QSF) as a subspace. Furthermore, let
 be a map so that be a map so that
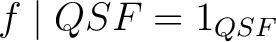 , with QSS being an arbitrary, local quantum state space (which is not necessarily finite). There exists an , with QSS being an arbitrary, local quantum state space (which is not necessarily finite). There exists an  -connected -connected  model (Z,QSF) for the pair (QSS,QSF) such that: model (Z,QSF) for the pair (QSS,QSF) such that:
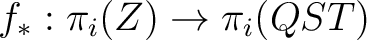 , ,
is an isomorphism for 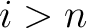 and it is a monomorphism for and it is a monomorphism for 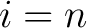 . The . The 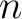 -connected -connected  model is unique up to homotopy equivalence. (The model is unique up to homotopy equivalence. (The 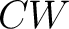 complex, complex, 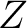 , considered here is a homotopic `hybrid' between QSF and QSS). , considered here is a homotopic `hybrid' between QSF and QSS).
Theorem 2. (Baianu, Brown and Glazebrook, 2007: In Section 9 of a recent NAQAT preprint). For every pair 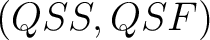 of topological spaces defined as in Lemma 1, with QSF nonempty, there exist of topological spaces defined as in Lemma 1, with QSF nonempty, there exist 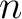 -connected -connected 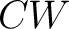 models models
 for all for all 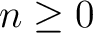 . Such models can be then selected to have the property that the . Such models can be then selected to have the property that the 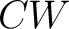 complex complex 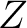 is obtained from QSF by attaching cells of dimension is obtained from QSF by attaching cells of dimension 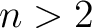 , and therefore , and therefore 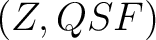 is is 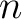 -connected. Following Lemma 01
one also has that the map: -connected. Following Lemma 01
one also has that the map:
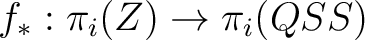 which is an isomorphism for which is an isomorphism for 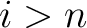 , and it is a monomorphism for , and it is a monomorphism for 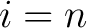 . .
Note See also the definitions of (quantum) spin networks and spin foams.
|
"CW-complex representation theorems in QAT" is owned by bci1.
|
|
| Other names: |
quantum algebraic topology (QAT) theorems for  -connected spaces -connected spaces |
| Keywords: |
CW-complex representation, spin networks and spin foams |
Cross-references: spin networks and spin foams, topological, homotopy, monomorphism, isomorphism, local quantum state space, QSS, quantum spin foams, spin networks, quantum state spaces, theorems, QAT
This is version 5 of CW-complex representation theorems in QAT, born on 2009-01-16, modified 2009-01-30.
Object id is 404, canonical name is CWComplexRepresentationTheorems.
Accessed 1313 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

