|
This article treats relations from the perspective of combinatorics, in other words, as a subject matter in discrete mathematics, with special attention to finite structures and concrete set-theoretic constructions, many of which arise quite naturally in applications. This approach to relation theory, or the theory of relations, is distinguished from, though closely related to, its study from the perspectives of abstract algebra on the one hand and formal logic on the other.
Two definitions of the relation concept are common in the literature. Although it is usually clear in context which definition is being used at a given time, it tends to become less clear as contexts collide, or as discussion moves from one context to another.
The same sort of ambiguity arose in the development of the function concept and it may save some effort to follow the pattern of resolution that worked itself out there.
When we speak of a function
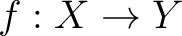 we are thinking of a mathematical object whose articulation requires three pieces of data, specifying the set we are thinking of a mathematical object whose articulation requires three pieces of data, specifying the set 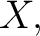 the set the set 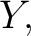 and a particular subset of their cartesian product and a particular subset of their cartesian product
 So far so good. So far so good.
Let us write
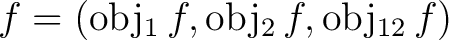 to express what has been said so far. to express what has been said so far.
When it comes to parsing the notation
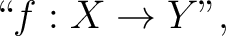 everyone takes the part everyone takes the part
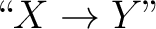 to specify the type of the function, that is, the pair to specify the type of the function, that is, the pair
 but but 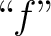 is used equivocally to denote both the triple and the subset is used equivocally to denote both the triple and the subset
 that forms one part of it. One way to resolve the ambiguity is to formalize a distinction between a function and its graph, letting that forms one part of it. One way to resolve the ambiguity is to formalize a distinction between a function and its graph, letting
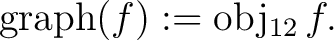
Another tactic treats the whole notation
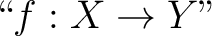 as sufficient denotation for the triple, letting as sufficient denotation for the triple, letting 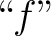 denote denote

In categorical and computational contexts, at least initially, the type is regarded as an essential attribute or an integral part of the function itself. In other contexts it may be desirable to use a more abstract concept of function, treating a function as a mathematical object that appears in connection with many different types.
Following the pattern of the functional case, let the notation
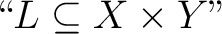 bring to mind a mathematical object that is specified by three pieces of data, the set bring to mind a mathematical object that is specified by three pieces of data, the set  the set the set 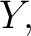 and a particular subset of their cartesian product and a particular subset of their cartesian product
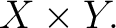 As before we have two choices, either let As before we have two choices, either let
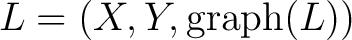 or let or let  denote denote
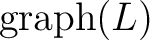 and choose another name for the triple. and choose another name for the triple.
It is convenient to begin with the definition of a 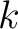 -place relation, where -place relation, where 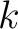 is a positive integer. is a positive integer.
Definition. A 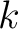 -place relation -place relation
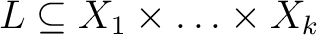 over the nonempty sets over the nonempty sets
 is a is a 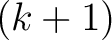 -tuple -tuple
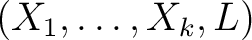 where where  is a subset of the cartesian product is a subset of the cartesian product
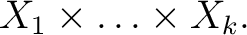
Though usage varies as usage will, there are several bits of optional language that are frequently useful in discussing relations. The sets
 are called the domains of the relation are called the domains of the relation
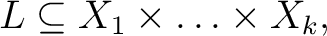 with with 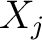 being the being the
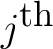 domain. If all of the domain. If all of the 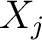 are the same set are the same set 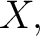 then then
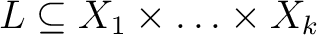 is more simply described as a is more simply described as a 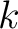 -place relation over -place relation over 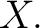 The set The set  is called the graph of the relation is called the graph of the relation
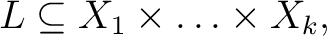 on analogy with the graph of a function. If the sequence of sets on analogy with the graph of a function. If the sequence of sets
 is constant throughout a given discussion or is otherwise determinate in context, then the relation is constant throughout a given discussion or is otherwise determinate in context, then the relation
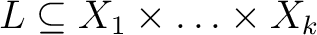 is determined by its graph is determined by its graph  making it acceptable to denote the relation by referring to its graph. Other synonyms for the adjective making it acceptable to denote the relation by referring to its graph. Other synonyms for the adjective  -place are -place are 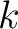 -adic and -adic and  -ary, all of which leads to the integer -ary, all of which leads to the integer 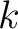 being called the dimension,
the adicity, or the arity of the relation being called the dimension,
the adicity, or the arity of the relation 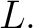
A local incidence property (LIP) of a relation 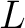 is a property that depends in turn on the properties of special subsets of is a property that depends in turn on the properties of special subsets of 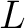 that are known as its local flags. The local flags of a relation are defined in the following way: that are known as its local flags. The local flags of a relation are defined in the following way:
Let 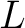 be a be a 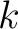 -place relation -place relation
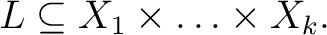
Select a relational domain 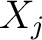 and one of its elements and one of its elements 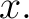 Then Then 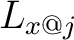 is a subset of is a subset of  that is referred to as the flag of that is referred to as the flag of  with with 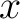 at at 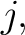 or the or the  -flag of -flag of 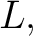 an object that has the following definition: an object that has the following definition:
Any property  of the local flag of the local flag
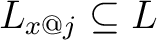 is said to be a local incidence property of is said to be a local incidence property of 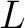 with respect to the locus with respect to the locus 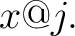
A 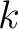 -adic relation -adic relation
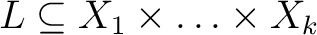 is said to be is said to be  -regular at -regular at 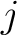 if and only if every flag of if and only if every flag of 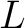 with with 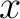 at at 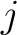 has the property has the property  where where 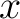 is taken to vary over the theme of the fixed domain is taken to vary over the theme of the fixed domain 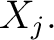
Expressed in symbols,  is is  -regular at -regular at 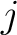 if and only if if and only if
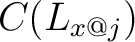 is true for all is true for all 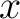 in in 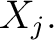
The definition of a local flag can be broadened from a point 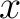 in in 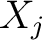 to a subset to a subset 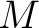 of of 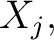 arriving at the definition of a regional flag in the following way: arriving at the definition of a regional flag in the following way:
Suppose that
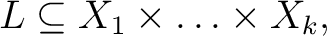 and choose a subset and choose a subset
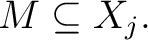 Then Then 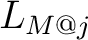 is a subset of is a subset of 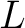 that is said to be the flag of that is said to be the flag of 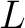 with with 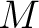 at at 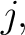 or the or the 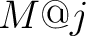 -flag of -flag of 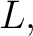 an object which has the
following definition: an object which has the
following definition:
A numerical incidence property (NIP) of a relation is a local incidence property that depends on the cardinalities of its local flags.
For example, 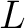 is said to be is said to be 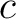 -regular at -regular at 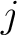 if and only if the cardinality of the local flag if and only if the cardinality of the local flag 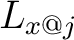 is is 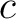 for all for all 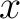 in in 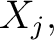 or, to write it in symbols, if and only if or, to write it in symbols, if and only if
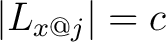 for all for all
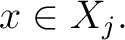
In a similar fashion, one can define the NIPs,  -regular at -regular at 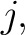 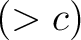 -regular at -regular at 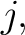 and so on. For ease of reference, a few of these definitions are recorded here: and so on. For ease of reference, a few of these definitions are recorded here:
Returning to 2-adic relations, it is useful to describe some familiar classes of objects in terms of their local and numerical incidence properties. Let
 be an arbitrary 2-adic relation. The following properties of be an arbitrary 2-adic relation. The following properties of  can be defined: can be defined:
If
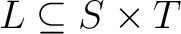 is tubular at is tubular at 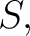 then then  is called a partial function or a prefunction from is called a partial function or a prefunction from 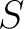 to to  This is sometimes indicated by giving This is sometimes indicated by giving 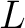 an alternate name, say, “ an alternate name, say, “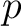 ", and writing ", and writing

Just by way of formalizing the definition:
If 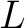 is a prefunction is a prefunction
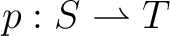 that happens to be total at that happens to be total at 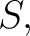 then then 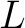 is called a function from is called a function from 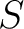 to to 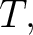 indicated by writing indicated by writing
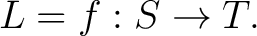 To say that a relation To say that a relation
 is totally tubular at is totally tubular at  is to say that it is is to say that it is 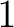 -regular at -regular at 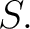 Thus, we may formalize the following definition: Thus, we may formalize the following definition:
In the case of a function
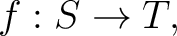 one has the following additional definitions: one has the following additional definitions:
Because the concept of a relation has been developed quite literally from the beginnings of logic and mathematics, and because it has incorporated contributions from a diversity of thinkers from many different times and intellectual climes, there is a wide variety of terminology that the reader may run across in connection with the subject.
One dimension of variation is reflected in the names that are given to 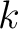 -place relations, for -place relations, for
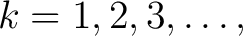 with some writers using the Greek forms, medadic, monadic, dyadic, triadic, with some writers using the Greek forms, medadic, monadic, dyadic, triadic,  -adic, and other writers using the Latin forms, nullary, unary, binary, ternary, -adic, and other writers using the Latin forms, nullary, unary, binary, ternary, 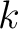 -ary. -ary.
The cardinality of the relational ground, the set of relational domains, may be referred to as the adicity, the arity, or the dimension of the relation. Accordingly, one finds a relation on a finite number of domains described as a polyadic relation or a finitary relation, but others count infinitary relations among the polyadic. If the number of domains is finite, say equal to  then the relation may be described as a then the relation may be described as a 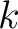 -adic relation, a -adic relation, a 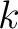 -ary relation, or a -ary relation, or a 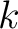 -dimensional relation, respectively. -dimensional relation, respectively.
A more conceptual than nominal variation depends on whether one uses terms like predicate, relation, and even term to refer to the formal object proper or else to the allied syntactic items that are used to denote them. Compounded with this variation is still another, frequently associated with philosophical differences over the status in reality accorded formal objects. Among those who speak of numbers, functions, properties, relations, and sets as being real, that is to say, as having objective properties, there are divergences as to whether some things are more real than others, especially whether particulars or properties are equally real or else which one is derivative in relationship to the other. Historically speaking, just about every combination of modalities has been used by one school of thought or another, but it suffices here
merely to indicate how the options are generated.
| 
