|
homotopy category
|
(Definition)
|
|
|
Let us consider first the category 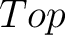 whose objects are topological spaces whose objects are topological spaces 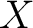 with a chosen basepoint with a chosen basepoint 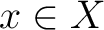 and whose morphisms are continuous maps and whose morphisms are continuous maps 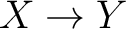 that associate the basepoint of that associate the basepoint of 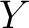 to the basepoint of to the basepoint of 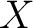 . The fundamental group of . The fundamental group of 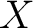 specifies a functor specifies a functor
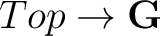 , with , with
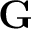 being the category of groups and group homomorphisms, which is called the fundamental group functor. being the category of groups and group homomorphisms, which is called the fundamental group functor.
Next, when one has a suitably defined relation of homotopy between morphisms, or maps, in a category 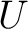 , one can define the homotopy category , one can define the homotopy category 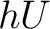 as the category whose objects are the same as the objects of as the category whose objects are the same as the objects of 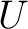 , but with morphisms being defined by the homotopy classes of maps; this is in fact the homotopy category of unbased spaces.
We can further require that homotopies on , but with morphisms being defined by the homotopy classes of maps; this is in fact the homotopy category of unbased spaces.
We can further require that homotopies on 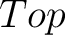 map each basepoint to a corresponding basepoint, thus leading to the definition of the homotopy category map each basepoint to a corresponding basepoint, thus leading to the definition of the homotopy category 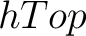 of based spaces. Therefore, the fundamental group is a homotopy invariant functor on of based spaces. Therefore, the fundamental group is a homotopy invariant functor on 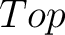 , with the meaning that the latter functor factors through a functor , with the meaning that the latter functor factors through a functor
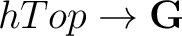 . A homotopy equivalence in . A homotopy equivalence in 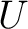 is an isomorphism in is an isomorphism in 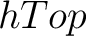 . Thus, based homotopy equivalence induces an isomorphism of fundamental groups.
In the general case when one does not choose a basepoint, a fundamental groupoid . Thus, based homotopy equivalence induces an isomorphism of fundamental groups.
In the general case when one does not choose a basepoint, a fundamental groupoid 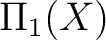 of a topological space of a topological space 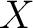 needs to be defined as the category whose objects are the base points of needs to be defined as the category whose objects are the base points of 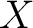 and whose morphisms and whose morphisms 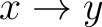 are the equivalence classes of paths from are the equivalence classes of paths from 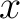 to to 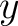 . .
- Explicitly, the objects of
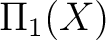 are the points of are the points of 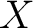
- morphisms are homotopy classes of paths “rel endpoints” that is
where,
 denotes homotopy rel endpoints, and, denotes homotopy rel endpoints, and,
- composition of morphisms is defined via piecing together, or concatenation, of paths.
Therefore, the set of endomorphisms of an object 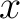 is precisely the fundamental group is precisely the fundamental group 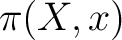 . One can thus construct the groupoid of homotopy equivalence classes; this construction can be then carried out by utilizing functors from the category . One can thus construct the groupoid of homotopy equivalence classes; this construction can be then carried out by utilizing functors from the category 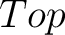 , or its subcategory , or its subcategory 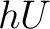 , to the category of groupoids and groupoid homomorphisms, , to the category of groupoids and groupoid homomorphisms, 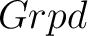 . One such functor which associates to each topological space its fundamental (homotopy) groupoid is appropriately called the fundamental groupoid functor. . One such functor which associates to each topological space its fundamental (homotopy) groupoid is appropriately called the fundamental groupoid functor.
As an important example, one may wish to consider the category of simplicial, or 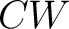 -complexes and homotopy defined for -complexes and homotopy defined for 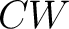 -complexes. Perhaps, the simplest example is that of a one-dimensional -complexes. Perhaps, the simplest example is that of a one-dimensional 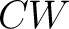 -complex, which is a graph. As described above, one can define a functor from the category of graphs, Grph, to -complex, which is a graph. As described above, one can define a functor from the category of graphs, Grph, to 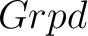 and then define the fundamental homotopy groupoids of
graphs, hypergraphs, or pseudographs. The case of freely generated graphs (one-dimensional and then define the fundamental homotopy groupoids of
graphs, hypergraphs, or pseudographs. The case of freely generated graphs (one-dimensional 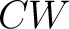 -complexes) is particularly simple and can be computed with a digital computer by a finite algorithm using the finite groupoids associated with such finitely generated -complexes) is particularly simple and can be computed with a digital computer by a finite algorithm using the finite groupoids associated with such finitely generated 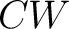 -complexes. -complexes.
Related to this concept of homotopy category for unbased topological spaces, one can then prove the approximation theorem for an arbitrary space by considering a functor
and also the construction of an approximation of an arbitrary space 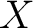 as the colimit as the colimit  of a sequence of cellular inclusions of of a sequence of cellular inclusions of 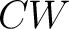 -complexes -complexes
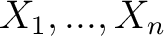 , so that one obtains , so that one obtains
![$X \equiv colim [X_i]$ $X \equiv colim [X_i]$](http://images.physicslibrary.org/cache/objects/719/l2h/img46.png) . .
Furthermore, the homotopy groups of the 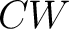 -complex -complex 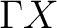 are the colimits of the homotopy groups of are the colimits of the homotopy groups of 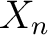 , and , and
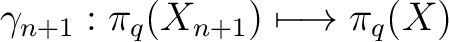 is a group epimorphism. is a group epimorphism.
- 1
- May, J.P. 1999, A Concise Course in Algebraic Topology., The University of Chicago Press: Chicago
- 2
- R. Brown and G. Janelidze.(2004). Galois theory and a new homotopy double groupoid of a map of spaces.(2004). Applied Categorical Structures,12: 63-80. Pdf file in arxiv: math.AT/0208211
|
"homotopy category" is owned by bci1.
|
|
| Also defines: |
fundamental group functor, homotopy classes of maps, fundamental groups |
| Keywords: |
homotopy category |
Cross-references: epimorphism, homotopy groups, approximation theorem for an arbitrary space, concept, algorithm, computer, hypergraphs, graph, simplicial, fundamental groupoid functor, groupoid homomorphisms, category of groupoids, groupoid, composition, fundamental groupoid, isomorphism, homotopy, relation, homomorphisms, groups, functor, fundamental group, morphisms, topological, objects, category
There are 14 references to this object.
This is version 1 of homotopy category, born on 2009-05-02.
Object id is 719, canonical name is HomotopyCategory.
Accessed 2000 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

